Найдите все значения параметра а , при каждом из которых наименьшее значение функции f(x) = ax+ |x^2 - 6x + 8| - 4а больше -1

(см. объяснение)

Пошаговое объяснение:

Заметим, что функция непрерывна и на бесконечностях стремится к плюс бесконечности. Тогда она имеет свой минимум при любом значении параметра.

Выполним наложение условия:

Нам надо найти такие значения параметра, чтобы это неравенство было истинно при любом значении переменной .

Откуда перейдем к более удобному виду:

Слева нет параметра. Тогда эту чисть неравенства построим в координатах (x; y), понимая, что она будет фиксирована.

Справа находится параметрическая прямая, вращающаяся вокруг точки (4; 0). Ее тоже строим в той же системе координат.

Тогда задача заключается в том, чтобы сделать так, когда вся левая часть неравенства находится выше прямой.

Покажем соответствующие расположения прямой:

(см. прикрепленный файл)

В первом случае, она касается параболы .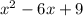

Тогда:

Здесь постороннее значение.

Во втором случае, прямая проходит через точку (2; 1).

Итого при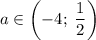 наименьшее значение функции больше минус одного.

Задание выполнено!