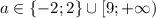найдите все значения параметра а для каждого из которых уравнение 9^x+(a-9)3^x=(5+2|a-1|)3^x+(a-9)(5+2|a-1|) имеет единственное решение
Другие вопросы по теме Математика
Популярные вопросы
- Найдите корни уровнений -2(x+3)=2x-1...
3 - Для чего была предпринята церковная реформа? назовите основные новшества,...
1 - Фонетический разбор 5 класса слова тяжкий...
3 - Корневую систему растений образуют какие корни?...
1 - Какую часть сутков составляет а) пять суток. б)шесть суток...
1 - :составьте 10 - 12 словосочетаний с не во всех частях речи (глагол , причастие...
2 - Какие действующие лица были в поеме илиада...
2 - Почему пушкин в рассказе станционный смотритель называет так своего героя?...
3 - Какие из отрезков ав мр сd оk еk равны,если ав=3см,мр=5см, сd=30мм,ок=50мм,еf=84см?...
2 - Подсчитай по календарю и сравни длительность светлого времени суток в эти...
3
Пошаговое объяснение:
Пусть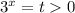 . Показательная функция — монотонно возрастающая, поэтому на количестве корней эта замена не сказывается (кроме t ≤ 0). Тогда
. Показательная функция — монотонно возрастающая, поэтому на количестве корней эта замена не сказывается (кроме t ≤ 0). Тогда
Заметим, что второй корень всегда положителен, то есть как минимум один корень у этого уравнения есть. Тогда другой корень должен быть либо неположительным, либо совпасть с первым.
В первом случае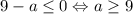 .
.
Во втором случае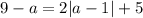
Если a ≥ 1, то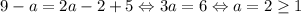
Если a < 1, то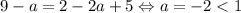
Таким образом,