Найдите все полиномы Р(x), для которых 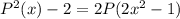
Другие вопросы по теме Математика
Популярные вопросы
- Фильм длится k часов и m минут. составьте линейный алгоритм перевода длительности...
1 - Как целое число 10 будет представлено в памяти компьютера в четырех байтах?...
3 - Вформулах, когда пишем вверху цифры со знаками + или -, когда мы пишем знак...
2 - Восьмая часть учащихся 4а класса. составляет 4человека. сколько всего учащихся...
2 - Решите неравенство 3^(x+4) +3^(-x-3) 4...
3 - Как понял паустовский выражение да солнце, да скроется тьма...
1 - (4*5-3): 2 в квадрате = (4*39-3): 3 в квадрате =...
3 - Древняя русь 3 класс доклад 5 октября 2016 года...
3 - Вторговом зале магазина выставили банки с вишневым малиновым и клубничным вареньем...
1 - Чему научился страшила пока сидел в в башне?...
1
Преобразуем: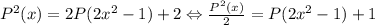 . Сделаем замену:
. Сделаем замену: 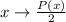 (полином имеет значение в любой точке), тогда:
(полином имеет значение в любой точке), тогда: 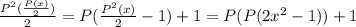 . Отсюда:
. Отсюда: 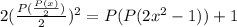 , поскольку
, поскольку 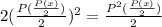 . Пусть
. Пусть 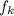 обозначает примененную
обозначает примененную 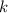 раз композицию функции
раз композицию функции 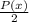 с самой собой. Аналогичным образом связана функция
с самой собой. Аналогичным образом связана функция 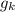 с функцией
с функцией 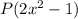 . Продолжая вышеуказанные подстановки, приходим к равенству
. Продолжая вышеуказанные подстановки, приходим к равенству 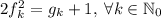 . Теперь:
. Теперь: 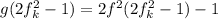 , поскольку
, поскольку 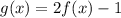 (здесь
(здесь 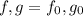 ). Но
). Но 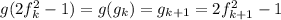 , значит,
, значит, 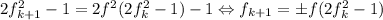 , но старший коэффициент
, но старший коэффициент 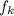 положителен, откуда
положителен, откуда 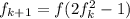 . Пусть старший коэффициент
. Пусть старший коэффициент 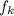 равен
равен 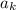 . Предположим, что
. Предположим, что 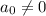 . Посчитаем старший коэффициент слева:
. Посчитаем старший коэффициент слева: 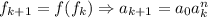 , где
, где 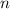 — степень многочлена
— степень многочлена 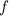 . Старший коэффициент справа равен старшему коэффициенту
. Старший коэффициент справа равен старшему коэффициенту 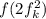 и равен
и равен 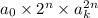 . Приравниваем:
. Приравниваем: 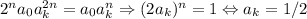 (поскольку
(поскольку 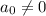 ). В частности,
). В частности, 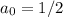 .
.
Заметим, что старший коэффициент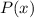 равен
равен 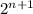 (в этом несложно убедиться). Тогда
(в этом несложно убедиться). Тогда 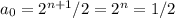 , но такого натурального
, но такого натурального 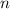 нет. Стало быть,
нет. Стало быть, 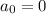 , то есть
, то есть 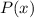 константа. Пусть
константа. Пусть 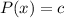 :
: 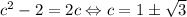 .
.