Найдите все натуральные х, для которых 3х+1 и 6х-2 - точные квадраты, а число 6*(x^2)-1 - простое.

Допустим, есть натуральное число n. Его квадрат -- это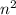 . По условию, 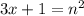и 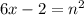. Так как правые части равны, приравняем левые части и найдём икс:

.

При x=1 получаем: 3*1+1=4 и 6*1-2=4. Четыре -- это точный квадрат двойки. А число 6*1*1-1=5 -- простое. Значит, число 1 удовлетворяет всем трём условиям.

Таких натуральных чисел больше не существует. При решении уравнения мы получили лишь один корень -- единицу. Можно методом подбора по ряду квадратов найти ещё корни. Какие-то из них будут соответствовать одному условию, какие-то -- одновременно двум (первому и второму, или первому и третьему, или второму и третьему). Но не найдётся ни одного числа, которое одновременно удовлетворяло бы сразу трём условиям.

ответ: x=1.