1. Математика
  2. найдите все четырехзначные

найдите все четырехзначные числа которые будучи выписаны три раза подряд образуют число кратное 14

прррр11 прррр11    1   08.06.2021 09:58    10

Ответы
Aliotu Aliotu  08.07.2021 10:59

Все четные четырехзначные числа

Пошаговое объяснение:

Пусть какое-либо из искомых четырехзначных чисел имеет вид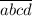 \overline{abcd}. Тогда, после применения указанной операции, будет получено число 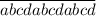\overline{abcdabcdabcd}, кратное 14.

Очевидно,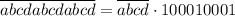 \overline{abcdabcdabcd}=\overline{abcd}\cdot 100010001.

Проверим делимость второго множителя на 7:

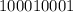100010001=100100000-89999=7*143*100000-70000-19999=7*143*100000-7*10000-21000+1001=7*143*100000-7*10000-7*3000+7*143=7*(143*100000-10000-3000+143)

То есть 100010001 делится на 7. Но, очевидно, на 2 не делится (т.к. нечетно). Значит, для делимости на 14=2*7 числа 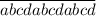\overline{abcdabcdabcd} необходимо и достаточно, чтобы 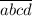\overline{abcd} делилось на 2.

То есть искомое множество чисел - все четные четырехзначные числа.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
meizum2luba meizum2luba  16.04.2020 12:59
Добавляли 200 г 10% раствора сахара и 300 г 20% раствора сахара. Какова концентрация полученного раствора сахара...
Сабина11123 Сабина11123  16.04.2020 12:59
и объяснить кто сможет. (не обязательно зарание с:​...
Gamonga Gamonga  16.04.2020 12:59
Раскрой скобки и у выражение: −6(5−a)+3(−2a−2)−7(−8+a)....
GriefSS GriefSS  16.04.2020 12:59
Решите эти 2 задачи и обратные задачи​...
юм123 юм123  16.04.2020 12:59
решите задания за все задания...
diasashat11 diasashat11  16.04.2020 12:59
Одна сторона прямоугольника равна 6дм, а другая в 4 раза меньше. Вычислил периметр прямоугольника​...
890605 890605  16.04.2020 12:59
Решение задач по теме «Призма»П.76. Решите задачу:Найти объем правильной n-угольной призмы, у которой каждое ребро равно8,если n=3n=4 n=6​...
aneechkaa000 aneechkaa000  16.04.2020 12:59
Коренем якого рівняння є число -3? 1) -2х - 5 =11 2) 3х +1 = - 8 3) 2(х - 4) = 5 4) 2х+4 = 7...
Sveta7102006 Sveta7102006  16.04.2020 12:59
Час розгону до 100 км/год одного автомобіля становить 19 с, а другого - 15,2 с. На скільки відсотків час розгону першого автомобіля більше, ніж другого ?​...
Yana6hhhh Yana6hhhh  16.04.2020 12:59
В правильном треугольнике случайно выбирают точку. Какова вероятность, что она окажется ближе к центру вписанной окружности, чем к границе треугольника?...

Популярные вопросы