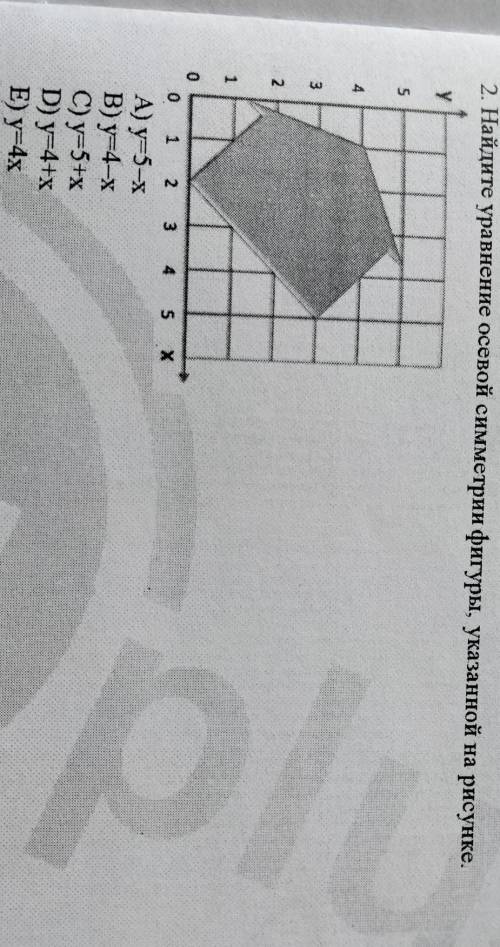
Найдите уравнение осевой симметрии фигуры, указанной на рисунке. А) y=5-х В) y=4-х C) y=5+x D) y=4+x E) y=4x

Для того чтобы найти уравнение осевой симметрии фигуры, мы должны найти ось симметрии, то есть линию, которая делит фигуру на две равные части, при этом каждая часть является зеркальным отражением другой.

На данном рисунке видно, что ось симметрии должна быть вертикальной линией, так как одна половина фигуры зеркально отражает другую по отношению к вертикальной линии. Вертикальная линия проходит через середину фигуры, которая является точкой пересечения двух сегментов с наклоном.

Чтобы найти координаты точки пересечения, нужно решить систему уравнений, составленных по уравнениям сегментов с наклоном.

Уравнение первого сегмента: y = 4 - х
Уравнение второго сегмента: y = 5 + x

Чтобы найти точку пересечения, мы должны приравнять оба уравнения и решить полученное уравнение:

4 - х = 5 + x

Суммируем х на обе стороны:

-х - х = 5 - 4

-2х = 1

Делим обе части на -2:

х = -1/2

Теперь мы найдем значение y, подставляя х = -1/2 в одно из уравнений:

y = 4 - (-1/2)
y = 4 + 1/2
y = 8/2 + 1/2
y = 9/2

Итак, точка пересечения равна (-1/2, 9/2).

Таким образом, ось симметрии проходит через точку (-1/2, 9/2).

Уравнение осевой симметрии можно записать в виде x = -1/2, так как все точки, которые находятся на этой линии, имеют одинаковую x-координату (-1/2), но разные y-координаты.

Следовательно, правильный ответ на задачу: А) уравнение осевой симметрии фигуры - x = -1/2