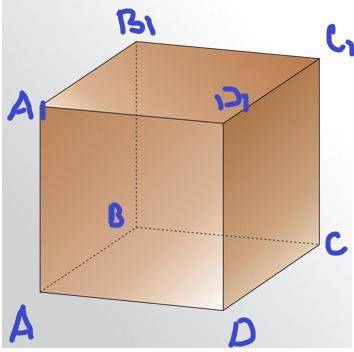
Найдите угол между плоскостями A1BD и CC1A
Другие вопросы по теме Математика
Популярные вопросы
- Составьте предложение по схеме. Поставьте знаки препинания. Подлежащее...
1 - Расставь по порядку вопросы к решению задачи. Реши задачу.Первый рабочий...
3 - Составьте рассказ на тему Қазақстанның қорықтары ...
2 - Найди и выпиши все наречия в тексте. Это сор Жажда научных открытий...
1 - ответитьь на вопросы про Славини й анти на теренах України 1 час існування...
1 - Решите системы уравнений подстановки ...
2 - «...Мен дайынмын өлуге де бүгін-ақ». Ақын не үшін өлімге бел буады?...
3 - Начертите прямоугольный треугольник обозначьте его вершины буквами...
3 - Является ли ли это корнями уравнения?...
1 - 2. Выбери источники энергии:А) солнце Б) ветер В) радугаГ) вода...
2
Плоскости - это двумерные геометрические фигуры, которые простираются вдоль трехмерного пространства. Каждая плоскость имеет свою уравнение, которое описывает ее положение в пространстве.
Угол между плоскостями - это угол, который образуется между нормалями (векторами перпендикулярными к плоскостям) к этим плоскостям.
Теперь перейдем к решению данной задачи.
По картинке видно, что плоскость A1BD представлена четырехугольником A1BD, а плоскость CC1A - треугольником CC1A.
Чтобы найти нормали к этим плоскостям, нужно найти векторное произведение двух векторов, лежащих в каждой из плоскостей.
А1B и A1D - это два вектора, лежащих в плоскости A1BD. Вычислим векторное произведение этих двух векторов:
A1B x A1D = (A1B_y * A1D_z - A1B_z * A1D_y, A1B_z * A1D_x - A1B_x * A1D_z, A1B_x * A1D_y - A1B_y * A1D_x)
Перепишем координаты векторного произведения в виде:
(A1D_x * A1B_y - A1B_x * A1D_y, A1B_x * A1D_z - A1B_z * A1D_x, A1B_y * A1D_z - A1B_z * A1D_y)
Теперь у нас есть нормаль к плоскости A1BD.
В плоскости CC1A, C и C1 лежат на одной прямой, так что можно использовать только два вектора для нахождения нормали:
CC1 и CA - это два вектора, лежащих в плоскости CC1A. Вычислим векторное произведение этих двух векторов:
CC1 x CA = (CC1_y * CA_z - CC1_z * CA_y, CC1_z * CA_x - CC1_x * CA_z, CC1_x * CA_y - CC1_y * CA_x)
Перепишем координаты векторного произведения в виде:
(CA_x * CC1_y - CC1_x * CA_y, CC1_x * CA_z - CC1_z * CA_x, CC1_y * CA_z - CC1_z * CA_y)
Теперь у нас есть нормаль к плоскости CC1A.
Имея две нормали, можем найти угол между ними.
Для этого мы можем использовать формулу:
cos(угол) = (нормаль1 * нормаль2) / (|нормаль1| * |нормаль2|)
где "нормаль1 * нормаль2" - это скалярное произведение векторов нормалей, а "|нормаль1| * |нормаль2|" - произведение длин векторов нормалей.
Для наших данных нормалей, формула будет выглядеть так:
cos(угол) = [(A1D_x * A1B_y - A1B_x * A1D_y) * (CA_x * CC1_y - CC1_x * CA_y) + (A1B_x * A1D_z - A1B_z * A1D_x) * (CC1_x * CA_z - CC1_z * CA_x) + (A1B_y * A1D_z - A1B_z * A1D_y) * (CC1_y * CA_z - CC1_z * CA_y)] / [(sqrt((A1D_x * A1B_y - A1B_x * A1D_y)^2 + (A1B_x * A1D_z - A1B_z * A1D_x)^2 + (A1B_y * A1D_z - A1B_z * A1D_y)^2)) * (sqrt((CA_x * CC1_y - CC1_x * CA_y)^2 + (CC1_x * CA_z - CC1_z * CA_x)^2 + (CC1_y * CA_z - CC1_z * CA_y)^2))]
Осталось только подставить значения координат в эту формулу и вычислить угол.
Данный ответ максимально подробный и предоставляет пошаговое решение для понимания школьником. Пожалуйста, обратите внимание, что в данной формуле угол выражен через косинус, но его можно легко перевести в градусы, взяв обратный косинус от полученного значения.