.Найдите угловой коэффициент касательной к графику функции y=3x3-x2-x-1 в точке х0 =1.

Ответы

CoJlne4Hblu 15.10.2020 14:28

k = 0

Пошаговое объяснение:

$f(x) = x^{3} - x^{2} - x - 1\\f'(x) = 3x^{2} - 2x - 1\\$

Мы знаем, что уравнение касательной к точке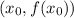 (x_0, f(x_0)) выражается в виде: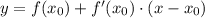 $y = f(x_0) + f'(x_0)\cdot(x - x_0)$

Наша точка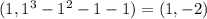 $(1, 1^{3} - 1^{2} - 1 - 1) = (1, -2)$

$y = -2 + (3\cdot1^{2} - 2\cdot1 -1)\cdot(x - 1) = -2 + (0)\cdot(x - 1) = -2$

Получается, наша касательная представляет собой горизонтальную прямую, и k = 0

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

INokentiy228 18.06.2019 13:40

уеее1 18.06.2019 13:40

Сравните числа а и б, если 5/7 числа а равны 15% числа б...

maximborisoc 18.06.2019 13:40

gramma116 18.06.2019 13:40

stasamaca 18.06.2019 13:40

Viktoria1289 18.06.2019 13:40

Сочини сказку почему у луні нет платья...

ldfjwdsrerwv 18.06.2019 13:40

rodionowa2003 18.06.2019 13:40

Сообщение по окр.мир сообщение о лесах россии...

larionxam 18.06.2019 13:40

Николь560 18.06.2019 13:40

900ц = т 7км207м= м 300дм= м 8т005кг= кг 5м30дм= дм 2ч45мин= мин...