Найдите точку минимума функции y=3х^2 – 12х+5.
Другие вопросы по теме Математика
Популярные вопросы
- 4 сынып қазақ тілі өтінем көмектесіңіздерші...
2 - Сторони прямокутника дорівнюють 10 м і 12 м. Знайдіть сторону квадрата, у...
3 - Приведение нескольких дробей к наименьшему общему знаменателю. Пример 2.47,34,514НОК(7;...
1 - Що називається частотою обертання тіла і як її обрахувати?...
1 - you are going to organise an event with your partner. Decide what kind of...
1 - Жырдағы Кенесары образы І.Есенберлиннің Көшпенділер трилогиясындағы Кенесары...
2 - 2) у = kx - 2 при k = 4;. Запишите формулу линейноїкает ось ординат в точке:...
3 - Подготовьте рассказ на основе литературного материала или жизненных наблюдений,...
2 - План: 1. Павлусь- хлопчик із козацької родини2. Ділова наука3. Дружба із...
2 - До розчину хлоридної кислоти масою 200г з масовою часткою кислоти 20% добавили...
2
ответ: точка минимума функции у=-7 при х=2.
Пошаговое объяснение:
Точка минимума функции - ее вершина(если коэффициент а положительный)
Чтобы найти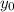 нужно подставить значение
нужно подставить значение 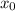
Точка минимума функции -- -7, при х=2