Найдите точку минимума функции, решить подробно
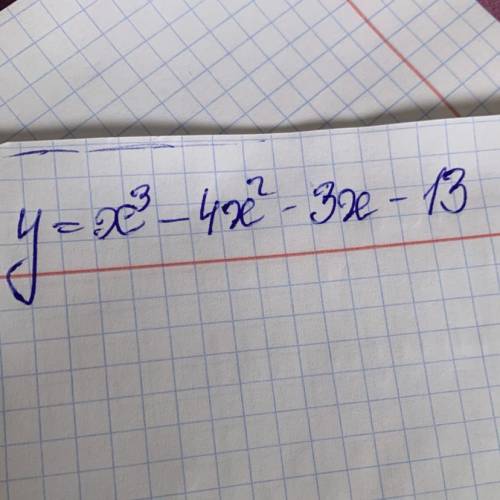
Другие вопросы по теме Математика
Популярные вопросы
- Творческое задание состав памяти путешественника на литература ...
3 - 1. Начертите отрезок AB длиной 12 cm и укажите точки D, E, F так, чтобы...
3 - составьте описание уголка одной из природных зон Украины 1)выберете...
3 - . очень нужно Книга-це(написати 7-9 речень) (ЗА ТВОРОМ 451°ЗА ФАРЕНГЕЙТОМ)...
1 - Самий довгий кораловий риф?...
3 - Реши систему уравнений.x- у - z = 0,х+ у - z = 6,x+y+z= 8....
3 - A regular polygon has an interior angle of 175°. How many sides does...
3 - Write questions in the present perfect. Example: we / finish / the checks?...
2 - Кто сможет мне ответить в ближайшее время, я ему добавлю ещё Как решать...
3 - диаметр кола описанного навколо прямокутного трикутника доривнюе 18...
2
Производная y' = 3x² – 8x – 3. Приравняем производную к нулю, найдем экстремумы и промежутки монотонности:
3x² – 8x – 3 = 0
D = (–8)² + 4·3·3 = 100 = 10²
x₁ = (8 – 10) / 6 = –1/3
x₂ = (8 + 10) / 6 = 3
Производная отрицательна на интервале (–1/3; 3), поэтому функция на этом интервале убывает и достигает локального минимума при x = 3.
y(3) = 3³ – 4·3² – 3·3 – 13 = 27 – 36 – 9 – 13 = –31
ответ: локальный минимум достигается в точке (3; –31).
ответ: хmin=3, уmin=27-36-9-13=-31, см фото
Пошаговое объяснение: