1. Математика
  2. Найдите точку максимума

Найдите точку максимума функции y=-x^2+18x-7 ​

Infinity167 Infinity167    1   07.10.2020 08:49    14

Ответы
Dasulya21 Dasulya21  07.10.2020 09:01

-74

Пошаговое объяснение:

Точка максимума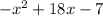 -x^2+18x-7 совпадает с точкой минимума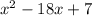 x^2-18x+7

Правило: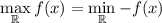 \displaystyle \max_{\mathbb{R}}f(x)=\min_{\mathbb{R}}-f(x)

Выделим полный квадрат

x^2-18x+7=x^2-18x+81-81+7=(x^2-18x+81)-74=(x-9)^2-74

Так как квадрат всегда не меньше 0, то квадрат - 74 не меньше -74, а значит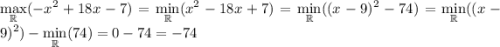 \displaystyle \max_{\mathbb{R}}(-x^2+18x-7)=\min_{\mathbb{R}}(x^2-18x+7)=\min_{\mathbb{R}}((x-9)^2-74)=\min_{\mathbb{R}}((x-9)^2)-\min_{\mathbb{R}}(74)=0-74=-74

ПОКАЗАТЬ ОТВЕТЫ
Lorosa Lorosa  07.10.2020 09:01

Пошаговое объяснение:y=-x²+18x-7--графиком явл. парабола,ветви направлены вниз с вершиной в точке с координатами х= - b/2a= -18/(-2)=9, y=-9²+18·9-7=-81+162-7=74;

A(9;74)--вершина параболы

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
nikitaknss nikitaknss  15.04.2021 22:24
В один поезд загрузили 120тон картофеля,а в другой 950тон.В одном поезде на 5вагоно больше чем в другом .Сколько вагонов в каждом поезде ,если в каждый вагон грузили одинаковое...
5мояоценка 5мояоценка  15.04.2021 22:28
» За три дня маляр покрасил 28 дверей. За первый день он покрасил 8 дверей, за второй — 9 дверей,а остальные двери он покрасил за третий день. Сколь-ко дверей покрасил...
Сонякака332 Сонякака332  15.04.2021 22:30
Решите эту систему наиболее рациональным методом....
соня7871 соня7871  15.04.2021 22:31
Среди выпускников одной школы 60% составляют девушки. 10% юношей и 20% девушек этого выпуска собираются вступать в гуманитарных вузов. Какова вероятность того, что наугад...
Dmitry228q Dmitry228q  15.04.2021 22:32
даю! Напишите с объяснением !...
PavlWhite249 PavlWhite249  15.04.2021 22:32
(Номер 12) запиши выражения и вычесли их значения: 1)сумму чисел 63 и 12 уменьшить в 3 раза 2)разность чисел 39 и 18 умножить на 4 3)Из числа 750твычесть частное чисел...
любимчик27 любимчик27  15.04.2021 22:32
Записать уравнение прямой пропорционально параллельной данной прямой (y=0,2x-3,6)...
АсяБру АсяБру  15.04.2021 22:33
1/4y+7=22−1/12y надо найти у ( /-это дробь)...
dl919879 dl919879  15.04.2021 22:33
За три тіжкні відремонтувалі 56 км дороги. За другий тиждень відремонтувалі у 2 рази больше, чем за перший, а за третій-на 8 км более, чем за перший. Скільки кілометрів...
вафелька6 вафелька6  16.12.2021 18:39
Решите Математика не обращать внимание на уже заполненные поля(они скорее всего сделаны не правильно переделать....

Популярные вопросы