1. Математика
  2. Найдите точку максимума функции

Найдите точку максимума функции у=-2х^3 +9x^2+3

Aiutka574 Aiutka574    2   03.10.2019 15:01    0

Ответы
olga7882 olga7882  09.10.2020 14:33

Точка (3; 30)

Пошаговое объяснение:

y = -2x^3 + 9x^2 + 3

Для нахождения экстремумов найдём производную:

y' = -6x^2 + 18x = -6x(x - 3)

В экстремумах функции производная обращается в ноль.Следовательно, экстремумы функции - точки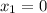 x_1 = 0 и x_2 = 3.

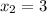Найдём вторую производную, чтобы понять чем является экстремум - локальным минимумом или локальным максимумом:

y'' = -12x + 18\\y''(x_1) = 18 0 \Rightarrow x_1 - \min\\y''(x_2) = -18 < 0 \Rightarrow x_2 - \max

Найдём значение в локальном максимуме:

y(x_2) = 30.

В качестве приложения - график:


Найдите точку максимума функции у=-2х^3 +9x^2+3
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
emilyrose2001 emilyrose2001  28.09.2019 08:30
Решить кубическую функцию, желательно подробно описывая действия, хочу понять суть. сама функция вот y=x^3+4x...
красотка248 красотка248  28.09.2019 08:30
Пролетая на драконе, гарри поттер увидел крысу рона, бегущую в противоположную сторону. пролетев ещё полминуты не меняя направления, гарри спрыгнул с дракона и отправился в погоню....
Natashazzz Natashazzz  28.09.2019 08:30
голодная гусеница составляет себе меню на ближайшие 8 дней. каждый день она хочет съесть один фрукт. у нее есть такой набор фруктов: груша, 4 яблока и 3 сливы. сколькими она может...
саяна7 саяна7  28.09.2019 08:30
Решить номер 35 1) 2-i : 1+i 2) i^10 * i^2...
Лена36793 Лена36793  28.09.2019 08:30
Куб состоит из 729 маленьких кубиков его расксили с внешней стороны и разобрали.сколько кубов разукрашено,хотя бы с одной стороны....
кирилл2071 кирилл2071  28.09.2019 08:30
Найти закономерность и продолжи ряд на три числа: 9,5,8,4,7,3, ....
zaydfudimp0dicv zaydfudimp0dicv  28.09.2019 08:30
Скажите сколько будет 1 1/9 минус 1/3...
ulya061 ulya061  28.09.2019 08:30
Известно, что х+1/х =11. чему равно х²+ 1/х²? , надо...
Abdresh Abdresh  28.09.2019 08:30
Укаждого учащегося в классе дома живет кошка или собака, а у некоторых, возможно, живет и кошка, собака. известно, что мальчиков, имеющих собак, не более 1/4 от общего числа учащихся,...
Arash12345 Arash12345  28.09.2019 08:30
Записали трехзначное число, все цифры которого одинаковые. оказалось, что это число делится на 9 . выделите цифры, которые могли быть использованы для записи этого числа. цифры: 123456789...

Популярные вопросы