1. Математика
  2. найдите сумму трёх чисел,

найдите сумму трёх чисел, первое из которых равно 4,2 а каждое следующее больше предыдущего на 3 2/3​

M10041999 M10041999    3   11.07.2021 19:09    1

Ответы
AlinaSmail76 AlinaSmail76  10.08.2021 19:46

26,3

Пошаговое объяснение:

переведем 4,2 в неправильную дробь: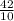 \frac{42}{10}

и 3 2/3 тоже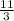 \frac{11}{3}

т.к знаменатели разные домножим первую дробь на 3 , а второю на 10

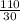
получим: \frac{126}{30} и \frac{110}{30}

значит второе число будет: \frac{126}{30} + \frac{110}{30} = \frac{236}{30}

значит третье число будет: \frac{236}{30} + \frac{110}{30} = \frac{346}{30}

найдем сумму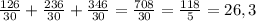 \frac{126}{30} + \frac{236}{30} + \frac{346}{30}=\frac{708}{30} =\frac{118}{5}=26,3

ПОКАЗАТЬ ОТВЕТЫ
ровно63 ровно63  10.08.2021 19:46

23.6

Пошаговое объяснение:

1-й :

1-е число

4.2 = 4\dfrac{1}{5}

2-е число

4\dfrac{1}{5} + 3\dfrac{2}{3} = 4\dfrac{3}{15} + 3\dfrac{10}{15} = 7 \dfrac{13}{15}

3-е число

7\dfrac{13}{15} + 3\dfrac{10}{15} =10\dfrac{23}{15} =11\dfrac{8}{15}

Сума трёх чисел

4\dfrac{3}{15} + 7 \dfrac{13}{15} + 11\dfrac{8}{15} =22\dfrac{24}{15} =23\dfrac{9}{15}=23\dfrac{3}{5} =23.6

2-й :

Арифметическая прогрессия

a_1 = 4.2 = 4\dfrac{1}{5}

d = 3\dfrac{2}{3}

a_3 = a_1 + 2d = 4\dfrac{1}{5} + 2\cdot 3\dfrac{2}{3} = 4\dfrac{1}{5} + 2\cdot \dfrac{11}{3} = 4\dfrac{1}{5} + \dfrac{22}{3} = \\ \\=4\dfrac{3}{15} + 7\dfrac{5}{15} =11\dfrac{8}{15}

S_3 = \dfrac{a_1+a_3}{2}\cdot3 = \dfrac{4\dfrac{3}{15} +11\dfrac{8}{15} }{2}\cdot3 = \\ \\=\dfrac{15\dfrac{11}{15} }{2}\cdot3 = \dfrac{\dfrac{236}{15} }{2}\cdot3 =\dfrac{236}{10} =23.6

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
vstef vstef  20.05.2020 13:27
Знайдіть значення х у пропорції: х+3/5=3/4та запишіть у відповіді число протилежне знайденому...
fghzghvyvvfsgv fghzghvyvvfsgv  20.05.2020 13:27
Дұрыс алты бұрышты призманың ең ұзын диагональі 8 см және олбүйір қырымен 30° бұрыш жасайды. Призманың көлемін есептеуплс...
Nice1111111111111 Nice1111111111111  20.05.2020 13:27
Прямокутник зі сторонами 2 і 5 см яка його площа і периметру?...
dfgery dfgery  20.05.2020 13:27
Трьом покупцям продали 23 кг помідорів . Перший купив 8 кг,а другий 6 кг помідорів . Скільки кілограмів помідорів купив 3 покупець треба)​...
Волк123111 Волк123111  20.05.2020 13:27
Швидкість потяга 75км за год.яку відстань він проїде за 3 години...
Ариша03072006 Ариша03072006  20.05.2020 13:27
F(x)=2-x Найти первообразную для функции...
McShram1111 McShram1111  20.05.2020 13:27
У выражение 2(3х – 1) - 4(2x + 3)​...
Ahau Ahau  20.05.2020 13:27
Решите систему линейных уравнений с двумя переменными сложения кто знает...
Софія133 Софія133  20.05.2020 13:27
В одном ящике 18 кг не очень вкусных яблок, что составляет ⅔ массы вкусных яблок, что находятся во втором ящике. Сколько килограмм яблок в обоих ящиках. *...
jkazlova jkazlova  20.05.2020 12:41
1. В пря¬мо¬уголь¬ном па¬рал¬ле¬ле¬пи¬пе¬де ABCDA1B1C1D1, у ко¬то¬ро¬го AB = 4, BC = 6, CC1 = 4, най¬ди¬те тан¬генс угла между плос¬ко¬стью ABC и пря¬мой EF, про¬хо¬дя¬щей...

Популярные вопросы