Найдите сумму неотрицательных целых решений неравенства: 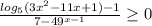$\frac{log_{5}(3x^2 -11x+1)-1}{7-49^{x-1} } \geq 0$

Ответы

seredinavi 06.08.2021 23:00

(см. объяснение)

Пошаговое объяснение:

$\dfrac{\log_5(3x^2-11x+1)-1}{7-49^{x-1}}\ge0$ , ОДЗ: $x\in\left(-\infty;\;\dfrac{11-\sqrt{109}}{6}\right)\cup\left(\dfrac{11+\sqrt{109}}{6};\;+\infty\right)$

Заметим, что исходному неравенству равносильно:

$\dfrac{3x^2-11x-4}{3-2x}\ge0,\;\;\dfrac{(3x+1)(x-4)}{2x-3}\le0$

По методу интервалов решением будет:

$x\in\left(-\infty;\;-\dfrac{1}{3}\right]\cup\left(\dfrac{3}{2};\;4\right]$

С учетом ОДЗ:

$x\in\left(-\infty;\;-\dfrac{1}{3}\right]\cup\left(\dfrac{11+\sqrt{109}}{6};\;4\right]$

Тогда сумма неотрицательных целых решений неравенства равна .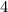

Задание выполнено!

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

viktoriabuble 06.06.2019 13:00

От пристани был спущен на воду плот, через 45 минут была спущена лодка с собственной скоростью 8 км/ч. какое расстояние, проплывет плот до того как его догонит лодка, если...

85Angel85 06.06.2019 13:00

Составь по краткой записи и реши её было 5книг и 9 книг взяли 4 книги осталось? 1 класс...

ress123 06.06.2019 13:00

35 ! нужно получить сочинение! написать сочинение на тему загрязнение воздуха или природы в россии...

Азик1166 06.06.2019 13:00

Из точки вне плоскости правильного шестиугольника имеющего площадь равную 96 корней из 3, к его вершинам проведены наклонные длиной 10 см определите на каком расстоянии...

Мику35 06.06.2019 13:00

Площадь опытного поля составляет 86 000 м2. часть этого поля, которая имеет форму прямоугольника со сторонами 240 м и 160 м, засеяна просом, а остальная площадь - гречихой....

laowiskskz 06.06.2019 13:00

Як зміниться добуток 9*а, якщо а збільшити в 3 рази, зменшити в 3 рази...

sdx2312 06.06.2019 13:00

Решите уравнения ! 22х+х-10=59 и 14у-2у+76=100...

Misterriko70 06.06.2019 13:00

Из 200 арбузов 16 оказались незрелыми. сколько процентов арбузов составили незрелые арбузы? 1) 16×100= - ? 2)1600÷200=8(℅) , мне надо узнать, какое наименование и пояснение...

Портнягин 06.06.2019 13:00

1. найдите объём прямоугольного параллелепипеда с измерениями 2 см , 8,1см и 0,5 см. 2. объём ёмкости , имеющей форму прямоугольного параллелепипеда , равен 40,575 м3 ....

shlykhta95 06.06.2019 13:00

Не знаю как составить краткую запись к : в первом куске было 24 м ткани, а во втором на 8 м меньше. из второго куска сшили одинаковые платья, расходуя на каждое по 4 м ткани....

Найдите сумму неотрицательных целых решений неравенства:

Популярные вопросы

Найдите сумму неотрицательных целых решений неравенства: $\frac{log_{5}(3x^2 -11x+1)-1}{7-49^{x-1} } \geq 0$