1. Математика
  2. Найдите сумму длин интервалов

Найдите сумму длин интервалов являющихся решениие неравенства

log4-x (5+x)<1

Настя123123ноно Настя123123ноно    1   28.07.2021 10:10    8

Ответы
jansayabektasova jansayabektasova  28.07.2021 10:20

log_{4-x}(5+x) 0\\4-x\neq 1\\5+x0x-5x \in (-5;3) \cup(3;4)\\\\log_{4-x}(5+x)-log_{4-x}(4-x)

По методу рационализации функция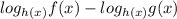 log_{h(x)}f(x)-log_{h(x)}g(x) с учетом ОДЗ принимает такие же знаки как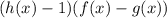  (h(x)-1)(f(x)-g(x))

\\(4-x-1)(5+x-(4-x))

(решение методом интервалов прикрепляю)

x \in (-5;-\frac{1}{2}) \cup(3;4)

Найдем сумму длин интервалов.

|-5+\frac{1}{2}|+|3-4|= 4,5+1=5,5


Найдите сумму длин интервалов являющихся решениие неравенстваlog4-x (5+x)<1
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Вика666666661 Вика666666661  19.08.2019 22:10
Вика сняла 4 фотографии а петя 2 сколько всего фотографий сделали дети 29...
gdhdf gdhdf  19.08.2019 22:10
Потрібно вирішити рівняння 72-54: с=66...
katyayatakozwmp5 katyayatakozwmp5  19.08.2019 22:10
Найдите сторону аd четырех угольника авсd описанного около окружности если ав=4, вс=5, сd=9...
жанна19882 жанна19882  19.08.2019 22:10
Постав запитання до і. розв яжи іі. на катку 6 хлопчиків грали хокей, а 4 дівчинки катались на ковзанах...
swordfishtrombone swordfishtrombone  19.08.2019 22:10
Запиши пропорцию: 9 так относится к 7,2, как 2 относится к 1,6....
Angela8689 Angela8689  19.08.2019 22:10
Автобус и автомобиль выехали одновременно из двух городов навстречу друг другу скорость автомобиля 70 км в час автобуса 60 километров час через сколько часов они встретятся...
максим885б максим885б  19.08.2019 22:10
Знаменатель дроби на 24 боль; ше ее числителя,a tak je v 2 raza bol she nego.naidi etu drob...
ek72Wasdk ek72Wasdk  19.08.2019 22:10
Несколько учеников внесли на покупку мяча по 40 руб. но оказалось что собранной суммы на 90 руб. меньше стоимости мяча когда же эти учащиеся собрали по 45 руб на собранной...
Elizzzavettta Elizzzavettta  19.08.2019 22:10
Не успела всё написать. решить эти уравнения x+2,8=3,72+0,38 4,1+у=20,3-4,9 z-6,8=8,7+6,4 10-v+4,3=10,7 всего 4 уравнения....
Mika123123 Mika123123  19.08.2019 22:10
Скласти план порівняльної характеристикиобразів тома й гека (твік пригоди тома сойяра )...

Популярные вопросы