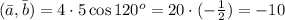Найдите скалярное произведение векторов a и b, если:

Другие вопросы по теме Математика
Популярные вопросы
- 1. Преобразуйте выражения: а) (с - 7)2; б) ( 3т + 1)(3т - 1)...
3 - 2тапсырма. Қысқаша берілген мәтінді түсініп,«төрт түлік» жануарлардың маңызы...
3 - решить английский нужно буду очень благодарен кто...
1 - 4. Докажите, что значение выражения: 1173 - 243 делится на 3 желательно в тетради...
1 - 1 что вы можете сказать о джетыасарской археологической культуре? 2 к какому...
3 - реши задачу школьники посадили 4 ряда яблонь по 10 деревьев и 2 ряда слив по...
3 - История Казахстана 5 класс сор...
2 - напишите правильно ответ это сор...
2 - В ПОСЛДГЕС ГЛАГОЛ shareокончание задания in brackets...
3 - Оцените степень плодородия земли в Новгороде ...
1
Пошаговое объяснение:
Скалярное произведение векторов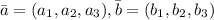 можно задать двумя
можно задать двумя
а)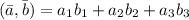
б)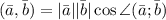
Для первых двух примеров считаем по первой формуле, для вторых двух примеров считаем по второй формуле:
1)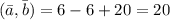
2)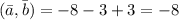
3)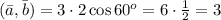
4)