Найдите sinx, если ctgx = - √3 и -π/2 < x < 0
Другие вопросы по теме Математика
Популярные вопросы
- 350 грамм стоят 300 рублей,как найти сколько стоит кг?...
2 - Площа ромба дорівнює 8см², а висота 2см. обчислити кути ромба...
3 - Объект (например, фрагмент текста или рисунок).попадает в буфер обмена...
3 - Является ли данная формула тождественно истинной, тождественно ложной,...
2 - Найдите значение выражения 2x0-3y0, где (x0; y0) – решение заданной системы...
2 - Решите ! 200 метров нити стоят 30 рублей. сколько тогда стоит : а) 1...
3 - Краткий пересказ а.с.пушкин барышня-крестьянка...
1 - А.свирский рыжик краткое содержание для читательского дневника( немного...
3 - 30 если . составь и записи предложения из отдельных слов. кормушку,серёжа,стали...
2 - Будет ли изомасляная кислота реагировать с уксусной кислотой? если да,...
1
Пошаговое объяснение:
Так как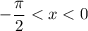 , то
, то 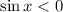
Основное тригонометрическое тождество: