Найдите шестнадцатый член последовательности (cn), заданной формулой cn= 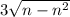$3 \sqrt{n - n {}^{2} }$

Question

Математика: Найдите шестнадцатый член последовательности (cn), заданной формулой cn= ​

tikatS66 · Answer

Чтобы найти шестнадцатый член последовательности (cn), заданной формулой cn= 3 * sqrt(n - n^2), нужно подставить значение n=16 в данную формулу и вычислить результат.

Подставляем значение n=16 в формулу:
c16 = 3 * sqrt(16 - 16^2)

Сначала вычисляем значение в скобках:
16 - 16^2 = 16 - 256 = -240

Затем вычисляем квадратный корень из полученного значения:
sqrt(-240) = NaN (не является числом)

Таким образом, мы не можем вычислить шестнадцатый член последовательности, так как значение под корнем отрицательное и лежит вне допустимого диапазона (для извлечения квадратного корня необходимо, чтобы значение под корнем было неотрицательным).

Ответ: шестнадцатый член последовательности не может быть вычислен.

Найдите шестнадцатый член последовательности (cn), заданной формулой cn= ​

Популярные вопросы

Найдите шестнадцатый член последовательности (cn), заданной формулой cn= $3 \sqrt{n - n {}^{2} }$