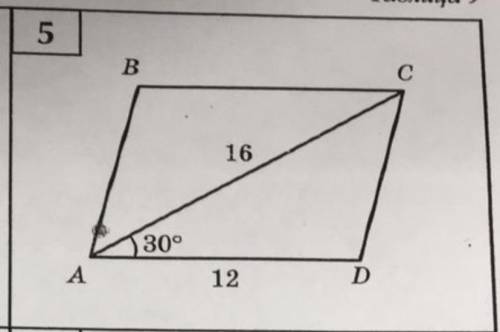
Найдите Sabcd
Это параллелограмм
, с объяснениями
Другие вопросы по теме Математика
Популярные вопросы
- Что чаще всего выражено глаголом. Оно также может быть выражено...
3 - 10 тетрадей разложили в 2 стопки сколько всего тетрадей 10:5=?...
2 - Прочитайте текст определите тему основную мысль целевую аудиторию...
1 - Определите вид треугольника АВС, еслиА(0;-2),В(-2;0),С(2;2)...
3 - -Қоқыс көп болмау үшін не істеу керек?...
2 - Отзыв о книге мой брат играет на кларнете...
2 - Записать в виде вариационного и статистического рядов выборку: 23,...
2 - Морфолический разбор слова Защищаешь...
1 - Придумать рекламу утюга ...
3 - Определите страну, о которой идёт речь.«Это островное государство....
2
ответ:96
Пошаговое объяснение:
СД=16:2=8(За властивістю прямокутного трикутника-катет прямокутного трикутника, що лежить проти кута 30°, дорівнює половині гіпотенуза)
СД=АВ=8
АД=ВС=12
S=12*8=96
1. Продлим сторону AD
2. Опустим перпендикуляр СF из вершины С на сторону АD
3. Построим высоту параллелограмма ВН ( для этого на сторону АD опустим перпендикуляр из вершины В)
• BHA и CFD прямоугольные треугольники, где АВ и СD - гипотенузы
4. Докажем, что треугольник BHA равен треугольнику СFD:
•AB=CD ( как противолежащие стороны параллелограмма)
• угол ВАН= углу СDF ( как соответствующие углы при параллельных прямых АВ и СF ( АВ||СF - по свойству параллелограмма) и секущей АF)
Треугольник ВНА = треугольнику СFD по гипотенузе и острому углу ( по признаку равенства прямоугольных треугольников)
5. BH= CF ( так как Треугольник ВНА = треугольнику СFD)
Найдём CF: рассмотрим прямоугольный треугольник АFC, где АС гипотенуза. CF = 16:2 = 8 ( как катет лежащий против угла в 30°). Значит ВН = 8.
6. Площадь параллелограмма находим по формуле: S = a•h:
Sabcd= AD• BH= 12•8= 96
ответ: 96