1. Математика
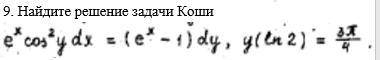
  2. Найдите решение задачи Коши

Найдите решение задачи Коши


Найдите решение задачи Коши

klevchuk71p06srz klevchuk71p06srz    3   28.06.2020 19:40    0

Ответы
Severelinka Severelinka  15.10.2020 15:02

y = \arctan(\log(e^x -1) - 1)Пошаговое объяснение:

Это ДУ уравнение с разделяющимися переменными

\frac{e^x dx}{e^x - 1} = \frac{dy}{\cos^2(y)}

\frac{d(e^x)}{e^x - 1} = \frac{dy}{\cos^2(y)}

проинтегрируем

\int \frac{d(e^x)}{e^x - 1} = \int \frac{dy}{\cos^2(y)}

\log(e^x - 1) = \tan(y) + C

Давайте воспользуемся условием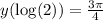 y(\log(2)) = \frac{3\pi}{4} чтобы найти константу:

\log(e^{\log(2)} - 1) = \tan(\frac{3\pi}{4}) + C

0 = -1 + C

C = 1.

То есть решение задачи коши такое:

\log(e^x - 1) = \tan(y) + 1,

можно оставить так (тогда у нас будет просто неявно заданная функция), а можно выразить отсюда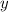 y:

y = \arctan(\log(e^x - 1) - 1)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Lololiplolpjvfhsbf Lololiplolpjvfhsbf  16.03.2022 15:25
Доклад на тему история возникновения отрицательных чисел (математика 6 класс)...
melochek228 melochek228  16.03.2022 15:26
Вова сделал 50 оборотов в прегулке. Что бы Вова получил Пятёрку ему нужно сделать 51 оборотов, а что бы получить четвёрку нужно 48 оборотов. Какую оценку должен теперь поставить...
Anna282005u Anna282005u  16.03.2022 15:28
5. Решите уравнение: 4 +5x-3=2x| =11...
ШаркоВалерия ШаркоВалерия  16.03.2022 15:29
В кулинарии используются меры: стакан, столовая ложка, чайная ложка. В таблице указана соответствующая данной мере масса продукта. Для приготовления одной порции каши нужно взять...
redf0x0 redf0x0  16.03.2022 15:36
Вероятность того, что лампочка останется исправной в течение года, равна 0,75. Найдите вероятность того, что в течение года а) из шести лампочек предстоит заменить ровно две лампочки;...
танэха танэха  16.03.2022 15:38
Вычислите 1)5\6+2\7 2)11\15-3\5 3)3\20+7\15 4)13\16-7\125)...
Elnur19982 Elnur19982  16.03.2022 15:38
(2x-5)2 в квадрате +(3x+5)+70x упростить выражение...
дарька4568 дарька4568  16.03.2022 15:48
ткань длиной 65 метров и шириной 1,25 метра стоит 37 500 сомов. сколько стоит ткань шириной 1,45 м и длиной 91 м?...
азаззазазаазз азаззазазаазз  16.03.2022 16:01
Упростить выражения(6 класс) с решением...
Aleks5953 Aleks5953  16.03.2022 16:12
Вычислить стороны параллелограмма, если диагонали равны 16 см и 18 см, а разность сторон 6 см....

Популярные вопросы