1. Математика
  2. Найдите радиус окружности описанной

Найдите радиус окружности описанной около треугольника со сторонами 18см 20 см и 34см

oaoaoaoaoa oaoaoaoaoa    2   14.09.2019 18:20    1309

Ответы
Vikzza Vikzza  07.10.2020 14:55
ответ:

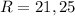R = 21,25 см.

Пошаговое объяснение:

Обозначим данный треугольник буквами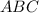 ABC

AB=20 см, AC = 18 см, BC = 34 см.

Начертим около данного треугольника окружность с центром в точке O.

R = \dfrac{AB \cdot BC \cdot AC}{4 \cdot S\triangle_{ABC}} (R - радиус описанной около \triangle ABC окружности с центром в точке O)

S_{\triangle ABC} = \sqrt{p\cdot(p - AB)\cdot(p - BC)\cdot(p - AC)}. (p - полупериметр \triangle ABC)

p = \dfrac{AB + BC + AC}{2} = \dfrac{20 + 34 + 18}{2} = 36 см

\Rightarrow S_{\triangle ABC} = \sqrt{36\cdot(36 - 20)\cdot(36 - 34)\cdot(36 - 18)} = 6\cdot4\cdot2\cdot3 = 144 см²

\Rightarrow R = \dfrac{18 \cdot 34 \cdot 20}{4 \cdot 144} = \dfrac{85}{4} = 21,25 см.


Найдите радиус окружности описанной около треугольника со сторонами 18см 20 см и 34см
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
2zeo915 2zeo915  13.02.2020 21:37
Одна минута разговора по мобильному телефону стоит 50 коп. Если разговаривать одну вторую часа в день, сколько придётся заплатить за неделю? За год? (Для удобства будем считать, что...
SuperSanii SuperSanii  13.02.2020 21:37
с задачкай проста братик отвликает...
rona3 rona3  13.02.2020 21:37
Задача Условия и решенийфермер продал 2 одинаковые по весу коровыи 4 обыкновеных бычка. общений массой 1828 кг масса одной коровы 286 кгкакова одного бычка​...
vborisenko75 vborisenko75  13.02.2020 21:38
Тапсырманы орында.Телефонды 7 4 және 9 цифрларынан тұратын кодпен батаудан шығаруға болады. Код 900-ден үлкен жұп сан екендігібелгілі. Кодты ата.​...
Костя228337 Костя228337  13.02.2020 21:38
9. Дано (1; -2), (3; 1), найти m,при котором векторы mä+b иä перпендикулярны и перпендикулярны....
2003Ivann 2003Ivann  13.02.2020 21:38
Упрости многочлен и найди его числовое значение: −ana+a2n4an+8,6, если a=4,n=1,7.Числовое значение многочлена равно​...
hellohelloschool hellohelloschool  13.02.2020 21:38
Умоляю нужно доказать тождество1)sin²α×sin²β+sin²α×cos²β+cos²α=12)cos2α/1+sin2α = 1-tgα/1+tgα...
ADAEV095 ADAEV095  13.02.2020 21:39
В классе 28 учащихся, четырет седьмых(4/7) из них девочки. Сколько мальчик ов в этом классе...
Фомида Фомида  08.08.2019 00:00
Какова сумма всех целых решений неравенства -92...
Kosmen21 Kosmen21  08.08.2019 00:00
Ұзындығы 18 м шілтерді өлшеуіш құралдарды пайдаланбай, қалайша ұзындықтары 15 м жəне 3 м бөліктерге бөлуге болады?...

Популярные вопросы