Найдите радиус окружности, описанной около треугольника, две стороны которого 5см и 8см, а угол между ними 60°.

Ответы

ktsimonsik 18.01.2022 19:29

Пошаговое объяснение:

по т.косинусов: с^2=а^2+в^2-2ав*cosC=25+64-40=49, значит с=7.

по т.синусов а/sinA=b/sinB=c/SinC=2R, значит 2R=14/√3

R=7/√3

как-то так)

перепроверь

ПОКАЗАТЬ ОТВЕТЫ

kusrik 18.01.2022 19:29

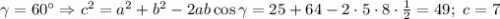
a=5; b=8; $\gamma=60^{\circ}\Rightarrow c^2=a^2+b^2-2ab\cos\gamma=25+64-2\cdot 5\cdot 8\cdot\frac{1}{2}=49;\ c=7$

(мы воспользовались теоремой косинусов). Далее, по теореме синусов,

$\dfrac{c}{\sin \gamma}=2R;\ R=\dfrac{7}{2\cdot \frac{\sqrt{3}}{2}}=\dfrac{7}{\sqrt{3}}=\dfrac{7\sqrt{3}}{3}.$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

kondan111 25.11.2021 17:40

Укажите верное неравенство если a 0, b 0, c 0...

latyshevavera2 25.11.2021 17:40

Kejiro 25.11.2021 17:40

milasuraeva 25.11.2021 17:40

Лана200611 25.11.2021 17:41

Вычисли (3,225-(-0,25)+2 3/4):(-14,65+28,4*(-8 1/8)...

angel150301 25.11.2021 17:41

Первообразная. Можно без решения...

MarinaRaim26 25.11.2021 17:41

MishaDunaev 25.11.2021 17:42

tskaev662 25.11.2021 17:42

succura 25.11.2021 17:42

Решите уравнение:3-x=2\7; x+2\9=5\6; x-1\6=3\8...