1. Математика
  2. Найдите радиус окружности

Найдите радиус окружности описанной около прямоугольника со сторонами 9 см и 12 см

varyuska varyuska    1   17.04.2022 09:42    5

Ответы
vladikkolbaska vladikkolbaska  17.04.2022 09:50

\Large r = 7,5 \: sm

Пошаговое объяснение:

Пусть прямоугольник вписанный в окружность будет АВСД.

Дано: BC=AD=12 см, ВА=СD=9 см.

Найти: r - окружности

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение

Диагональ делит прямоугольник на равные части, таким образом образовалось две прямоугольных треугольников. Диагональ прямоугольника является гипотенузой трегольников и диаметром окружности. Диагональ прямоугольника вычесляется по теореме Пифагора.

Формула:

\Large \boxed{d = \sqrt{{a}^{2} + {b}^{2}} }

Где а и b стороны прямоугольника.

\large d = \underset{ \large\sqrt{144 + 81} }{\underbrace{ \sqrt[]{ {12}^{2} + {9}^{2} } }} \: \: \Rightarrow \: \: \sqrt{144 + 81} = \underset{ \large15}{ \underbrace{ \sqrt{225} }} \\

Длина диагонали равна 15 см.

Если диагональ прямоугольника является ещё и диаметром окружности, то знаем, что радиус равняется половине диаметра.

Формула:

\Large \boxed{r = \frac{D}{2} }

Следовательно:

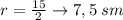
\large r = \frac{15}{2} \rightarrow7,5 \: sm

ответ: r = 7,5 см
Найдите радиус окружности описанной около прямоугольника со сторонами 9 см и 12 см
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
bkmz987 bkmz987  25.08.2019 08:30
Вычислите площадь основания прямоугольного параллелепипеда по данному объёму v=340,6дм, и высоте h=6,5дм...
Egor456803 Egor456803  25.08.2019 08:30
Стороны двух подобных параллелограммов относятся как 2: 3 найдите площадь меньшего параллелограмма если площадь большего параллелограмма равна 54 см²...
алина3539 алина3539  25.08.2019 08:30
Какое число больше 28 на 12, какое число меньше 47 на 42?...
Messi1444 Messi1444  25.08.2019 08:30
Кнаполовину заполненному баку вместимостью 2100л подведена труба, через которую наливается по230л воды каждый час. на дне бака образовалось отверстие, через которое каждый...
Govnoegc Govnoegc  25.08.2019 08:30
Суравнениями 15х=0,15; 3,08 : у =4; 3а + 8а = 1,87; 7z - 3z= 5,12; 2t+5t+3,18=25,3...
Кристиналадату Кристиналадату  25.08.2019 08:30
P= 22дм. ширина = 7 дм . s-? по действиям...
AliceMagic AliceMagic  25.08.2019 08:30
На фотовыставке 700цветных снимков в чёрно_белых на 480 меньше сколько всего снимков было на фотовыставке....
Мандариин1335 Мандариин1335  25.08.2019 08:30
Всказочной стране распродажат.васелиса купила ,3 скатерти свмобранки по 50 монет 2 шапки неведимки по 18 монет и волшеб палочку которая стоила в 2 ращв меньше чем шапки...
fariii046 fariii046  25.08.2019 08:30
Здвох міст назустріч один одному одночасно виїхали автобус і автомобіль. швидкість автомобіля 80км\год а швидкість автобуса становить 3\4 швидкості автомобіля. через...
volgakup volgakup  25.08.2019 08:30
Вираз 1)-2*(2х-у-3)-2*(2х-у)= 2)2х*(3b+5c)-x*(2a-4b)=...

Популярные вопросы