1. Математика
  2. Найдите промежуток убывания

Найдите промежуток убывания функции > f(x)=4х^3-12х+5
полное решение!

IVANICH31 IVANICH31    3   29.06.2020 11:29    0

Ответы
TheArinaS TheArinaS  15.10.2020 15:03
Решение:

Для начала найдём производную данной функции:

\boxed{f(x)=4{x}^{3}-12x+5} \\ \\ f'(x)=(4{x}^{3}-12x+5)'=(4{x}^{3})'-(12x)'+(5)'=3\cdot4{x}^{3-1}-12\cdot1+0=\boxed{12x^2-12}

Теперь найдём критические точки, приравнивая производную к нулю:

12{x}^{2}-12=0 \\ \\ 12x^2=12 \\ \\ x=\pm 1

Итак критические точки: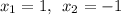 x_1=1, \: \: x_2=-1.

Устанавливаем знак производной на каждом интервале (см рисунок).

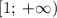Функция возрастает на каждом из промежутков (-\infty; \: -1] и [1; \: +\infty).

То есть функция убывает на промежутке \boxed{[-1; \: 1]}.

ответ: \Large{\boxed{[-1; \: 1]}}
Найдите промежуток убывания функции > f(x)=4х^3-12х+5полное решение!
Найдите промежуток убывания функции > f(x)=4х^3-12х+5полное решение!
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Dianochkach Dianochkach  24.02.2021 19:05
Gee on wryodul 7 wrodоu анəməО91-st uxodkwoessowordsandwodouooteatrudwadeog​...
никусь2222 никусь2222  24.02.2021 19:05
Запишите программный код для вычисления выражения: (х+55)/4*х вообще не шарю Делацте по примеру на картинке​...
559858 559858  24.02.2021 19:04
с решением задач. A(1,3) B(4,-5) P(3,7)...
chip0523 chip0523  24.02.2021 19:04
6. Обчисли зручним 25 12 4 15 17 3949Р 1;3907Tцінший варіант відповіді:90527. Знайдивід​...
Христинияголовн Христинияголовн  24.02.2021 19:04
Скоротіть будь ласка дріб даю за це ів...
MtDew557723 MtDew557723  24.02.2021 19:03
А че тут делать :_/\ если шо 4 класс​...
danilru940Vova danilru940Vova  24.02.2021 19:03
10-4x 3-3 x 2x-0,25x 3,5 за ответ...
лиана252 лиана252  24.02.2021 19:03
Как решить - 2 - 3 +44 (математика 6 клас) ​...
АЙДЫН261 АЙДЫН261  24.02.2021 19:03
Найдите частное 2) 2.08 : 0.05;3) 86.1: 0.41;5) 0.29: 0.05;6) 20,3 : 1.45:8) 0.016 : 0,0839) 2,244 : 5.61.столбиком сфоткамте зделал...
aliya77usa aliya77usa  24.02.2021 19:03
909. Вычислите только это ​...

Популярные вопросы