Найдите производную.
первый вариант, заранее
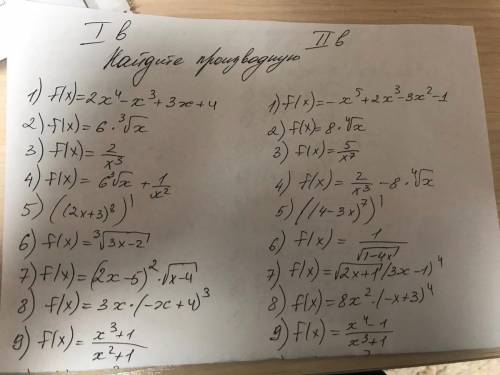
Другие вопросы по теме Математика
Популярные вопросы
- решить данное уравнение :б) 1,2х + 4,5х = 1,71.Буду благодарна....
3 - Русская народная пословица гласит: «Все хорошо, что хорошо кончается». Продолжи...
2 - На прямой отметили две красные точки и несколько синих. Оказалось, что одна...
3 - 1. Які функції виконує банк? 2. Чому заощадження родини краще зберігати в банку?...
3 - Сообщение по биологии водная среда 5 класс...
2 - Какое новое содержание музыки Бетховена отразилось на её в форме...
3 - Захопивши Україну, окупаційні війська знищили її цілісність та поділили її окупаційні...
1 - Стороны угла А касаются окружности с центром ора-диуса r. Найдите: а) ОА, если...
1 - Водные слова. Какую роль выполняют вводные слова и предложения? Отметьте номера...
2 - Тарас Бульба Н. Гоголь ( название, автор, герои, тема, основная мысль, чему...
3
2 вариант: