Найдите производную функции
y=3x^5-20x^2+8x+1
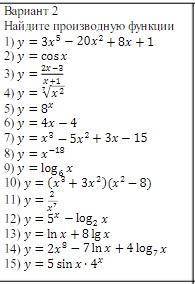
Другие вопросы по теме Математика
Популярные вопросы
- Сколько процентов число 7 от числа 12...
3 - Фонетический разбор сгибать ...
3 - Расчитать плотность населения армении, санкт-петербурга, москвы...
3 - 5. чому дорівнює ширина ріки, якщо звук з іншого берега дійшов...
2 - Для функции f(x) и g(x) запишите формулы и область определения...
1 - Длина прямоугольника — 84 см. ширина составляет 2/7 длины. найди,...
2 - 1.как отреагировали дети , когда увидели елку? 2. чем она была...
1 - Св колледж. 100 . из всей контрольной отсталость одно . две...
2 - D: put the world in the correct order to make sentences и e:...
3 - Начать сочинение на тему: книги которые меня вдохновляют...
3
Для слагаемого 3x^5:
У каждого слагаемого степень переменной указывает, как нужно умножить его на коэффициент перед ним, чтобы получить производную. Таким образом, производная слагаемого 3x^5 будет равна 5 * 3 * x^(5 - 1) = 15x^4.
Для слагаемого -20x^2:
Применяем аналогичное правило и получаем производную -20 * 2 * x^(2 - 1) = -40x.
Для слагаемого 8x:
Так как коэффициент перед переменной равен 8, производная будет равна 8.
Для слагаемого 1:
Константы не влияют на производную функции, поэтому производная будет равна 0.
Теперь сложим все эти производные, чтобы получить итоговую производную функции:
15x^4 - 40x + 8 + 0 = 15x^4 - 40x + 8.
Итак, производная функции y=3x^5-20x^2+8x+1 равна 15x^4 - 40x + 8.
ответ : y'=15х^4-40x+8