Найдите производную функции y=arcsin ln2x
Другие вопросы по теме Математика
Популярные вопросы
- Вообше не понимаю( атом у которого на внешнем электронном слое число пар спаренных...
3 - Сообщение об арктических пустынях ....
3 - На диске 6 мультфильмов .вчера дети посматрели 3 из них,а остальные сегодня...
3 - Поставить глаголы в нужном времени: he usually (do) his homework in the evening...
3 - Выполнить действия 8м4см-5дм= и 2м7см+38см=...
2 - Форма аквариума имеет обьём 0.125 м в кубе.каковы измерения этого аквариума?...
1 - Выполните действие : (- 1/2x^2y^3)^3*0.8xy^4...
3 - 1. кругла да гладка, откусишь - сладка. засела крепко на грядке . 2. ду-ду,...
3 - Найти длину окружности и площадь круга, если диаметр равен 8....
2 - Решить уравнения. б) 16-z(2 степень)=0 в)x(2 степень)-8x+16=0 г)t(5 степень)=...
2
Пошаговое объяснение:
Нужно взять производную сначала от арксинуса.
Это будет
Теперь возьмем производную от логарифма. Получим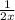
Осталось взять производную от выражения под логарифмом.
Это будет 2.
Теперь все это нужно перемножить по правилам взятия производной от сложной функции.
Это и будет искомой производной.
Пошаговое объяснение:
y=arcsin(ln(2x))
(arcsinx)'=1/√(1-x²) ⇒
y'=arcsin(ln(2x)'=(1/√(1-ln²(2x))*(ln(2x))'*(2x)'=
=(1/√(1-ln²(2x))*(1/(2x))*2=1/(x*√(1-ln²(2x)).