Найдите производную функции y=3sin3x в точке 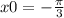
а)4,5;
б) -9;
в) -4, 5;
г) свой ответ
найдите промежутки убывания функций
а)(- ∞;0) промежуток (6;∞) ;
б) (0;6) ;
в) (0;3) промежуток (3;6) ;
г) свой ответ
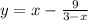
Другие вопросы по теме Математика
Популярные вопросы
- За октябрь земля сделает оборот вокруг своей воображаемой оси?...
1 - Придумать свои философские вопросы ? 3-4...
2 - Решите пример 12÷7,5+7,5÷12+0,25÷0,4×(5,1-3,86)= снизу примера решение...
1 - Образовать от существительного лес глагол....
2 - Решить .координаты: x=40+2t-4t^2. найти v( p.s v- здесь скорость....
1 - Поставь вопросы к выделенным словам: 1. he will read the letters tomorrow....
1 - Ее красиво оформляют и вешают на стену...
1 - Как организмы могут использовать уже отмершие клетки? примеры....
1 - Определите сколько лет с начала великих открытий до настоящего времени?...
1 - В4 одинаковых банках m литров сока. сколько литров сока в 9 таких банках....
3
1) Найдем производную функции y = 3sin(3x). Чтобы найти производную функции, нужно использовать правило дифференцирования для функции синус: производная синуса равна косинусу умноженному на производную аргумента. То есть, производная функции y = 3sin(3x) равна 3cos(3x) * производная аргумента (по правилу дифференцирования сложной функции).
Поскольку аргумент функции равен 3x, мы должны найти производную этого аргумента. Для этого умножим 3 на производную x, которая равна 1.
Получаем, что производная аргумента 3x равна 3.
Теперь мы можем записать полную производную функции y = 3sin(3x): y' = (3cos(3x))*(3).
Далее мы должны найти значение производной функции в заданной точке x₀ = -π/3. Подставляем это значение в формулу производной и рассчитываем:
y'(x₀) = (3cos(3*(-π/3)))*(3) = (3cos(-π))*3 = (3*(-1))*3 = -9.
Таким образом, производная функции y = 3sin(3x) в точке x₀ = -π/3 равна -9.
2) Теперь рассмотрим задание по поиску промежутков убывания функции y = x - 9/(3 - x).
Для начала найдем область определения функции. Очевидно, что знаменатель 3 - x не может быть равен нулю, поэтому исключаем этот случай. Имеем условие: 3 - x ≠ 0. Решим его:
3 - x ≠ 0
x ≠ 3.
Таким образом, область определения функции - это все значения x, кроме x = 3.
Теперь необходимо найти производную функции y = x - 9/(3 - x). Рассчитаем ее по правилу дифференцирования линейной функции:
y' = 1 - [(-9)*(-1)] / (3 - x)².
Приведем производную функции к общему знаменателю и упростим выражение:
y' = (3 - x)² + 9 / (3 - x)² - 9 / (3 - x)² = (3 - x)² / (3 - x)² = 1.
Получили, что производная функции y = x - 9/(3 - x) равна 1.
Теперь найдем критические точки функции, то есть значения x, при которых производная равна нулю или не существует. В данном случае, производная всегда равна 1, поэтому нет критических точек.
Теперь осталось рассмотреть поведение функции в разных интервалах.
a) Рассмотрим интервал (-∞;0). Подставим х = -1 в функцию:
y = -1 - 9/(3 - (-1)) = -1 - 9/4 = -1 - 2.25 = -3.25.
Значение функции меньше нуля. Значит, на этом интервале функция убывает.
б) Рассмотрим интервал (0;6). Подставим х = 1 в функцию:
y = 1 - 9/(3 - 1) = 1 - 9/2 = 1 - 4.5 = -3.5.
Значение функции меньше нуля. Значит, на этом интервале функция убывает.
в) Рассмотрим интервал (0;3). Подставим х = 2 в функцию:
y = 2 - 9/(3 - 2) = 2 - 9/1 = 2 - 9 = -7.
Значение функции меньше нуля. Значит, на этом интервале функция убывает.
г) Оставим этот вариант открытым для тебя. Ты можешь самостоятельно подставить значения в функцию и определить, растет ли или убывает функция на этом интервале.
Таким образом, ответы на задачи:
1) Производная функции y = 3sin(3x) в точке x₀ = -π/3 равна -9.
2) Промежутки убывания функции y = x - 9/(3 - x):
а) (-∞;0) промежуток (6;∞),
б) (0;6),
в) (0;3) промежуток (3;6),
г) твой ответ.
Надеюсь, что ответы понятны и помогут тебе разобраться в задачах! Если у тебя есть вопросы, не стесняйся задавать их. Удачи!