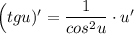Найдите производную функции y=1/2tg(4x-π)+π/4 при x=π/4
Другие вопросы по теме Математика
Популярные вопросы
- Выполни сложение 1/z+g+3zg/z^3+g^3 Последнее задание!...
1 - Я правда буду благодарна Прикреплено......
2 - очень За не правильные ответы буду банить! Буду очень благодарна...
2 - Коли на обличчі Холмса «з’являвся вираз внутрішньої вдоволеності»,-це означало...
2 - ответь на во по *Майская ночь или утопленница* 1) как Левко и Ганна относятся...
1 - Вычисли корень уравнения: 12,3−y=0,9....
3 - Об єм мурашиного альдегіду 56м³ Яка його маса в кг? 2.Між моментом відкриття...
3 - Изобразите схемы трёх логических элементов и подпишите (напишите название) каждый...
1 - Запитання 1 Обчисліть суму кутів опуклого n- кутника, якщо n=22 варіанти відповідей...
1 - 1 рівень 1.Любов матері до Павлуся в (Скарб)?- 2.Господар,в хаті якого жила ,мишка...
1
Сначала упростим функцию, применив формулы приведения. Затем воспользуемся правилом дифференцирования сложной функции: