1. Математика
  2. Найдите производную функции u=x*y^2

Найдите производную функции u=x*y^2 + z^3 - x*y*z в точке m(1,1,2) в направлении вектора (вект)i + sqrt(2)*(вект)j + (вект)k

Danelpos Danelpos    1   15.07.2019 13:00    0

Ответы
RonaAnna RonaAnna  20.09.2020 23:17
Совершаю ошибку, надо сначала проверить, является ли функция тотально дифференцируемой, но что же делать.
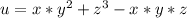
u = x*y^{2} + z^{3} - x*y*z
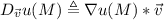
D_{\vec{v}}u(M) \triangleq \nabla u(M) * \vec{v}
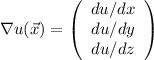
\nabla u(\vec{x}) = \left(\begin{array}{c} du/dx \\ du/dy \\ du/dz \end{array}\right)
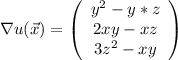
\nabla u(\vec{x}) = \left(\begin{array}{c} y^{2} - y*z\\ 2xy - xz \\ 3z^{2}-xy \end{array}\right)
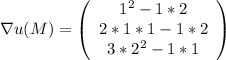
\nabla u(M) = \left(\begin{array}{c} 1^{2} - 1*2\\ 2*1*1 - 1*2 \\ 3*2^{2}-1*1 \end{array}\right)
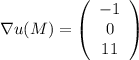
\nabla u(M) = \left(\begin{array}{c} -1\\ 0 \\ 11 \end{array}\right)
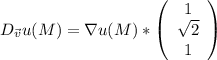
D_{\vec{v}}u(M) = \nabla u(M) * \left(\begin{array}{c} 1 \\ \sqrt{2} \\ 1 \end{array}\right)
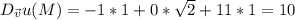
D_{\vec{v}}u(M) = -1 * 1 + 0 * \sqrt{2} + 11 * 1 = 10
ПОКАЗАТЬ ОТВЕТЫ
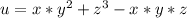
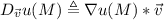
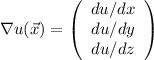
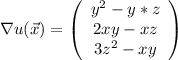
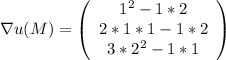
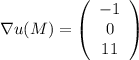
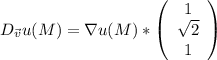
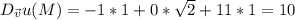
Другие вопросы по теме Математика
ананастенька21000 ананастенька21000  14.01.2021 21:43
2 1/3х + 1 1/2 = 1 2/3х решить ​...
24j18g81B 24j18g81B  14.01.2021 21:43
Діаметр круга дорівнює 18 см. Знайдіть площу кола​...
LLLLLina LLLLLina  14.01.2021 21:44
Найдите неизвестный член пропорции: ха)43x х12г)1824°б) 30: х = 2:25;х18д)0,55в) 8:7 = 112 : x;е) 1:1,8 = x дам пять звёзд, очень устала не могу сделать, кто нибудь...
Верониккка00 Верониккка00  14.01.2021 21:44
ДО ТЬ З САМОСТІЙНОЮ Завдання на фото...
Лубаша Лубаша  14.01.2021 21:44
6a+11a+15=321 и 16c-c+14=299...
Викa2003648219 Викa2003648219  14.01.2021 21:45
Знайдіть довжину кола, якщо його радіус дорівнює 5 см....
baller59 baller59  14.01.2021 21:46
Какой путь пройдет конец часовой стрелки в течение дня,если её длина 1.5 см(СПОЛНЫМ ОБЪЯСНЕНИЕМ )...
кристина2156 кристина2156  14.01.2021 21:46
Знайдіть бічну сторону рівнобедриного трикутниика основа якого 16 см а висота 15 см...
erkr erkr  14.01.2021 21:48
Вечером температура была -15,5°С а на протяжении всей ночи снизилась на 8°С...
bektursun bektursun  14.01.2021 21:48
Напишите сочинение про Влада Цепеш господаря Валахии в 7-6 предложении. СТАВЛЮ ВСЕ ЗВЁЗДЫ....

Популярные вопросы