1. Математика
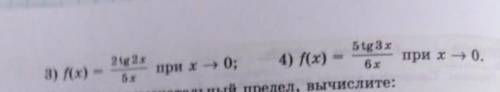
  2. Найдите предел функции умоляю​

Найдите предел функции
умоляю​


Найдите предел функции умоляю​

уяеный222 уяеный222    3   13.12.2020 13:45    0

Ответы
xujixixud xujixixud  12.01.2021 13:47

\frac{4}{5}; \quad \frac{5}{2};

Пошаговое объяснение:

3) \quad \lim_{x \to 0} \frac{2tg 2x}{5x};

Имеем неопределённость вида

\frac{0}{0};

Находим предел по методу Лопиталя. Для этого находим производные числителя и знаменателя дроби:

\lim_{x \to 0} \frac{2tg 2x}{5x}=\lim_{x \to 0} \frac{(2tg 2x)'}{(5x)'}=\lim_{x \to 0} \frac{2 \cdot (tg 2x)'}{5}=\lim_{x \to 0} \frac{2 \cdot (tg 2x)' \cdot (2x)'}{5}=

=\lim_{x \to 0} \frac{2 \cdot \frac{1}{cos^{2}(2x)} \cdot 2}{5}=\lim_{x \to 0} \frac{4}{5cos^{2}(2x)}=\lim_{x \to 0} \frac{4}{5 \cdot cos^{2}0}=\lim_{x \to 0} \frac{4}{5 \cdot 1}=\frac{4}{5};

4) \quad lim_{x \to 0}\frac{5tg 3x}{6x};

Имеем неопределённость вида

\frac{0}{0};

Решаем этот пример аналогично предыдущему:

\lim_{x \to 0} \frac{5tg 3x}{6x}=\lim_{x \to 0} \frac{(5tg 3x)'}{(6x)'}=\lim_{x \to 0} \frac{5 \cdot (tg 3x)'}{6}=\lim_{x \to 0} \frac{5 \cdot (tg 3x)' \cdot (3x)'}{6}=

=\lim_{x \to 0} \frac{5 \cdot \frac{1}{cos^{2}(3x)} \cdot 3}{6}=\lim_{x \to 0} \frac{5}{2cos^{2}(3x)}=\lim_{x \to 0} \frac{5}{2 \cdot cos^{2}0}=\lim_{x \to 0} \frac{5}{2 \cdot 1}=\frac{5}{2};

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Tumanovaad12 Tumanovaad12  23.08.2019 01:10
Веревка длиной 3 метров найди длину 5 восьмых части веревки...
Мировец2003 Мировец2003  23.08.2019 01:10
Впервый поезд загрузили 1200т зерна,а во второй -950т. в первом поезде было на 5 вагонов больше,чем во втором.сколько вагонов было в каждом поезде.если в каждый вагон...
alina15299 alina15299  23.08.2019 01:10
Найди значение выражений 145*26*13-23463: 11...
atom33 atom33  23.08.2019 01:20
Масса банки заполненная медом доверху, равна 850г., а заполненная на половину-550г. чему равнп масса самой банки? реши , рассмотрев схему целое часть...
ekozhushkova ekozhushkova  23.08.2019 01:20
Длина ручки : 10 см или 10 дм, длина коридора: 8 м или 80 см,ширина 4 дм или 4 м,высота: 2 м или 10 дм?...
chalavek chalavek  23.08.2019 01:20
Число, выражающее площадь прямоугольной комнаты в м2, на единицу больше числа, выражающего периметр этой комнаты в м. каковы размеры комнаты, если её длина и ширина...
Аленушка54545454 Аленушка54545454  23.08.2019 01:20
(x-1)(2x-3) 0 x квадрат-1 +2x+1. =1 x x {x-y=4 {xy=5...
аянаайши аянаайши  23.08.2019 01:20
От гриби до чернички воробей сделал 3 прыжка а от чернички до соснавой ишишки на 4 прыжка больше.сколко всего прыжков воробей сделал от гриба до шишки?...
juliakovta juliakovta  23.08.2019 01:20
Скорость велосепидиста 12км/ч.это в3раа больше скорости пешехода ,но в 6 раз меньше скорости автобуса . найди скорость пешехода и автобуса. большое...
2vovanavi 2vovanavi  23.08.2019 01:20
Первое число в 3 раза больше второго если от первого числа отнять 18 а ко второму прибавить 6 то получиться равные результаты...

Популярные вопросы