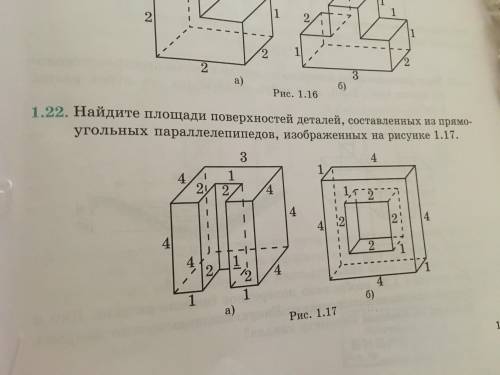
Найдите площади поверхностей деталей, составленных из прямоугольных параллелепипедов, изображенных на рисунке (б с подробным объяснением((

Хорошо, давайте разберем этот вопрос пошагово.

На рисунке мы видим два прямоугольных параллелепипеда, каждый из которых состоит из шести поверхностей. Нам нужно найти площади этих поверхностей.

Начнем с первого параллелепипеда, обозначенного буквой "а".

1. Первая поверхность параллелепипеда а - это передняя или фронтальная поверхность. Она имеет форму прямоугольника, для которого нужно найти площадь. Чтобы найти площадь прямоугольника, нужно умножить его длину на его ширину. По рисунку, длина прямоугольника равна 5 единицам, а ширина равна 4 единицам. Таким образом, площадь первой поверхности параллелепипеда "а" равна 5 * 4 = 20 квадратных единиц.

2. Вторая поверхность параллелепипеда "а" - это задняя или задняя поверхность. Она также имеет форму прямоугольника, поэтому площадь ее можно найти так же, как и первой. Длина прямоугольника равна 5 единицам, а ширина та же самая - 4 единицы. Следовательно, площадь второй поверхности параллелепипеда "а" также равна 5 * 4 = 20 квадратных единиц.

3. Третья поверхность параллелепипеда "а" - это верхняя поверхность. Она имеет форму прямоугольника, поэтому ее площадь можно найти как произведение длины и ширины. На рисунке, длина прямоугольника равна 3 единицам, а ширина - 4 единицы. Таким образом, площадь третьей поверхности параллелепипеда "а" равна 3 * 4 = 12 квадратных единиц.

4. Четвертая поверхность параллелепипеда "а" - это нижняя поверхность. Она также имеет форму прямоугольника и ее площадь можно найти так же, как третью поверхность. Длина прямоугольника равна 3 единицам, а ширина - 4 единицы. Следовательно, площадь четвертой поверхности параллелепипеда "а" равна 3 * 4 = 12 квадратных единиц.

5. Пятая поверхность параллелепипеда "а" - это левая боковая сторона. Она также имеет форму прямоугольника и ее площадь можно найти таким же образом, как первые четыре поверхности. Длина прямоугольника равна 3 единицам, а высота (высота параллелепипеда) равна 5 единицам. Следовательно, площадь пятой поверхности параллелепипеда "а" равна 3 * 5 = 15 квадратных единиц.

6. Шестая поверхность параллелепипеда "а" - это правая боковая поверхность. Она также имеет форму прямоугольника и ее площадь можно найти таким же образом, как первые пять поверхностей. Длина прямоугольника равна 3 единицам, а высота (высота параллелепипеда) также равна 5 единицам. Следовательно, площадь шестой поверхности параллелепипеда "а" равна 3 * 5 = 15 квадратных единиц.

- Общая площадь всех поверхностей параллелепипеда "а" равна сумме площадей всех его поверхностей. То есть 20 + 20 + 12 + 12 + 15 + 15 = 94 квадратных единиц.

Теперь перейдем ко второму параллелепипеду, обозначенному буквой "б".

1. Первая поверхность параллелепипеда "б" - это передняя или фронтальная поверхность. Она имеет форму прямоугольника. Длина прямоугольника равна 6 единицам, а ширина равна 3 единицам. Таким образом, площадь первой поверхности параллелепипеда "б" равна 6 * 3 = 18 квадратных единиц.

2. Вторая поверхность параллелепипеда "б" - это задняя или задняя поверхность. Она также имеет форму прямоугольника. Длина прямоугольника равна 6 единицам, а ширина такая же - 3 единицы. Следовательно, площадь второй поверхности параллелепипеда "б" также равна 6 * 3 = 18 квадратных единиц.

3. Третья поверхность параллелепипеда "б" - это верхняя поверхность. Она также имеет форму прямоугольника. Длина прямоугольника равна 3 единицам, а ширина равна 6 единицам. Следовательно, площадь третьей поверхности параллелепипеда "б" равна 3 * 6 = 18 квадратных единиц.

4. Четвертая поверхность параллелепипеда "б" - это нижняя поверхность. Она также имеет форму прямоугольника. Длина прямоугольника равна 3 единицам, а ширина такая же - 6 единиц. Следовательно, площадь четвертой поверхности параллелепипеда "б" равна 3 * 6 = 18 квадратных единиц.

5. Пятая поверхность параллелепипеда "б" - это левая боковая поверхность. Она также имеет форму прямоугольника. Длина прямоугольника равна 6 единицам, а высота (высота параллелепипеда) равна 4 единицы. Следовательно, площадь пятой поверхности параллелепипеда "б" равна 6 * 4 = 24 квадратных единиц.

6. Шестая поверхность параллелепипеда "б" - это правая боковая поверхность. Она также имеет форму прямоугольника. Длина прямоугольника равна 6 единицам, а высота (высота параллелепипеда) также равна 4 единицы. Следовательно, площадь шестой поверхности параллелепипеда "б" равна 6 * 4 = 24 квадратных единиц.

- Общая площадь всех поверхностей параллелепипеда "б" равна сумме площадей всех его поверхностей. То есть 18 + 18 + 18 + 18 + 24 + 24 = 120 квадратных единиц.

Итак, мы рассмотрели оба прямоугольных параллелепипеда и нашли площади всех их поверхностей.

Надеюсь, эта подробная информация помогла вам понять, как найти площади поверхностей прямоугольных параллелепипедов на данном рисунке. Если у вас возникнут еще вопросы, не стесняйтесь задавать их.