1. Математика
  2. Найдите площадь треугольника,

Найдите площадь треугольника, вершины которого имеют координаты (1; 6), (10; 6), (10; 8).

Bel4onokk Bel4onokk    1   30.06.2019 23:10    1

Ответы
диван111111 диван111111  02.10.2020 16:41
Вычислим длины сторон треугольника:
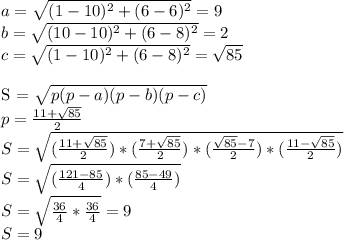
a = \sqrt{(1 - 10)^2 + (6 - 6)^2} = 9 \\
b = \sqrt{(10 - 10)^2 + (6 - 8)^2} = 2 \\
c = \sqrt{(1 - 10)^2 + (6 - 8)^2} = \sqrt{85} \\

S = \sqrt{p(p-a)(p-b)(p-c)} \\
p = \frac{11 + \sqrt{85} }{2} \\
S = \sqrt{(\frac{11 + \sqrt{85} }{2})*(\frac{7 + \sqrt{85} }{2})*(\frac{\sqrt{85} - 7}{2})*(\frac{11 - \sqrt{85} }{2})} \\
S = \sqrt{ (\frac{121 - 85}{4})*(\frac{85- 49}{4}) } \\
S = \sqrt{ \frac{36}{4}* \frac{36}{4} } = 9 \\
S = 9
ПОКАЗАТЬ ОТВЕТЫ
nikita200310266xcute nikita200310266xcute  02.10.2020 16:41
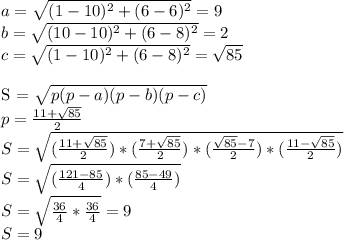
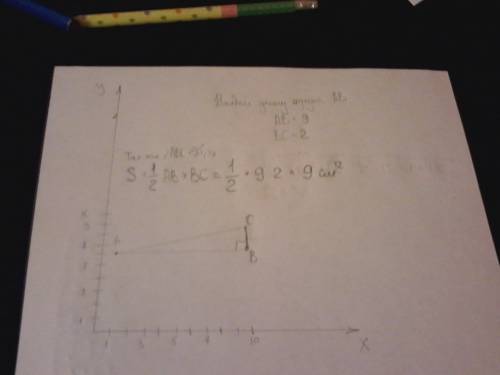
Эта же задача,только графически
Найдите площадь треугольника, вершины которого имеют координаты (1; 6), (10; 6), (10; 8).
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
rumtum rumtum  30.07.2019 21:00
1). решите систему уравнений: {5x + 3y = 4 2x - y = - 5 2). за 3 тетради и 5 карандашей саша заплатил 29 рублей, а таня за 1 тетрадь и 7 карандашей – 31 рубль. сколько стоит...
Василиса73 Василиса73  30.07.2019 21:00
Решите уравнение 2x-1,3+1,5=7,2 вычисли 32% от 124...
Виктория58928663 Виктория58928663  30.07.2019 21:00
Mолю о в какое время угол между часовой и минутной стрелками больше: в 10 ч или в 3 ч 30 минут? на сколько градусов?...
leedercools leedercools  30.07.2019 21:00
Сколько четерёхзначных чисел можно составить из цифр 3,5,7 и 8,если цифры в числе не повторяются?...
slipnot174 slipnot174  30.07.2019 21:00
Умоляю решить уравнение 7,3x+2,7x+35=321,8...
lkQwertyuiop1 lkQwertyuiop1  30.07.2019 21:00
Свежая ромашка содержит 88% воды, а сушеная – 25%. сколько получится сухой ромашки из 400 кг свежей?...
dkhairov1993 dkhairov1993  30.07.2019 21:00
4x+5=-5x-4 числа с х в одну сторону, и без икс в другую...
taidakv taidakv  30.07.2019 21:00
Что представляет собоц на современном этапе терроризм как общественное явление...
naystya6768oz59bt naystya6768oz59bt  30.07.2019 21:00
Стальная деталь массой 20 килограмм при обработке на токарном станке нагрелась на 50 градусов удельная теплоемкость стали составляет 46 килоджоулей на сколько при этом увеличилась...
Ріo78 Ріo78  30.07.2019 21:00
Какие виды стопорение болтов и гаек вы знаете...

Популярные вопросы