1. Математика
  2. Найдите площадь трапеции

Найдите площадь трапеции у которой параллельные стороны 60 см и 20 см а непараллельные 13 см и 37 см

maksategemberdi maksategemberdi    3   24.08.2019 08:20    1

Ответы
livr5 livr5  08.09.2020 23:59

Продлим стороны до параллелограмма AFCD; FA = CD = 37 см и FC = AD = 60 см. Отрезок FB = FC - BC = 60 - 20 = 40 см. Найдем площадь треугольника AFB по формуле Герона:

\rm p=\dfrac{FA+FB+BA}{2}=\dfrac{37+40+13}{2}=45 см - полупериметр

\rm S_{AFB}=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{45\cdot(45-40)\cdot(45-37)\cdot(45-13)}=\\ \\ =\sqrt{45\cdot5\cdot8\cdot32}=\sqrt{3^2\cdot5^2\cdot8^2\cdot2^2}=3\cdot5\cdot8\cdot2=240~_{CM^2}


С другой стороны площадь треугольника равна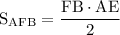 \rm S_{AFB}=\dfrac{FB\cdot AE}{2} откуда высота 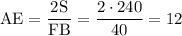\rm AE=\dfrac{2S}{FB}=\dfrac{2\cdot240}{40}=12 см. Высота треугольника AFB равна высоте трапеции, тогда


\rm S_{ABCD}=\dfrac{AD+BC}{2}\cdot AE=\dfrac{60+20}{2}\cdot12=480 см²



ответ: 480 см².


Найдите площадь трапеции у которой параллельные стороны 60 см и 20 см а непараллельные 13 см и 37 см
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
nazarm378 nazarm378  11.12.2020 15:15
Умножение обыкновенных дробей и смешанных чисел. Взаимно обратные числа. Урок 2 Вычисли значение выражения наиболее удобным ответ: Назад Проверить а то Математичка сожрёт меня...
makatova051 makatova051  11.12.2020 15:15
Задание 10 ответ волшебные точки...
AlexWhite472 AlexWhite472  11.12.2020 15:15
Математика 3 класс 10 задание...
Aigggggg Aigggggg  11.12.2020 15:15
Памагите паже и чтоб была все​...
karinaflyg karinaflyg  11.12.2020 15:16
Х+у=10 (100х+10у+7)-(10х+у)=259...
elizabetfox1222 elizabetfox1222  11.12.2020 15:16
S=(10см×5см):2=?S=(8см×10см): 2=? S=(4см×8см): 2=? ​...
dashagorbunova5 dashagorbunova5  11.12.2020 15:16
лимоны раскладывали в корзины по 100 штук в каждую Сколько было лимонов если Их разложили в 15 корзин и ещё осталось 30 Лимонов​...
алина3798 алина3798  11.12.2020 15:16
Найдите наибольший общий делитель 72 108 и 144...
Timurrovt456 Timurrovt456  08.06.2019 11:40
Решить . квадрат со стороной 4 см разрезали на 2 равных треугольника. чему равна площадь каждого треугольника? решение....
1234567891248 1234567891248  08.06.2019 11:40
Таксист за месяц проехал 6000 км .стоимость 1 литра бензина 21.5 рублей.средний расход бензина 100 км составляет 7 литров.сколько рублей потратил таксист на бензин за месяц...

Популярные вопросы