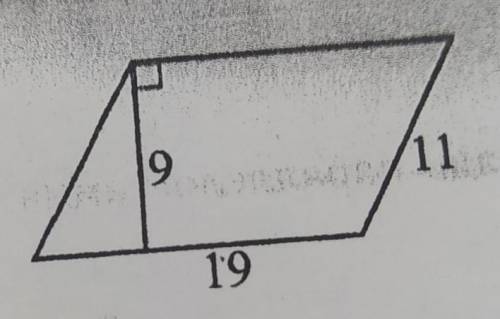
Найдите площадь палеограма изоброжлного на ресунке​

Для того чтобы найти площадь палеограма, нам нужно разбить его на более простые фигуры, для которых мы можем использовать знакомые нам формулы площади.

На рисунке видно, что палеограм состоит из двух треугольников и двух прямоугольников. Давайте найдем площадь каждой из этих фигур по очереди.

1. Треугольник ABC:
Для нахождения площади треугольника, нам нужно знать его высоту и основание. Основание треугольника — это отрезок AB, который имеет длину 6 см. Высоту можно найти, проведя перпендикуляр из вершины C к основанию AB.
Для этого нам нужно воспользоваться теоремой Пифагора. Из рисунка видно, что отрезок BC равен 8 см, а отрезок AC равен 10 см. По теореме Пифагора, квадрат гипотенузы (отрезка BC) равен сумме квадратов катетов (отрезка AB и отрезка AC). Используя эту формулу, мы можем найти высоту треугольника:
BC^2 = AB^2 + AC^2
8^2 = 6^2 + 10^2
64 = 36 + 100
64 = 136
Высота треугольника BC равна √64, что равно 8 см.
Теперь мы можем найти площадь треугольника по формуле: половина произведения основания на высоту.
Площадь треугольника ABC равна (1/2) * 6 * 8 = 24 кв.см.

2. Прямоугольник BDEH:
Длина прямоугольника BDEH равна 6 см, так как это основание треугольника ABC. Ширина прямоугольника равна высоте треугольника CDEJ. Мы уже нашли высоту в предыдущем расчете, это 8 см.
Для нахождения площади прямоугольника нам нужно умножить его длину на ширину.
Площадь прямоугольника BDEH равна 6 * 8 = 48 кв.см.

3. Треугольник DEF:
Этот треугольник имеет основание DE, которое равно 6 см. Высоту треугольника мы можем найти, опять используя теорему Пифагора.
Из рисунка видно, что отрезок DF равен 13 см, а отрезок EF равен 12 см.
Применяя теорему Пифагора, мы находим, что высота треугольника DF равна √(13^2 - 12^2) = √(169 - 144) = √25 = 5 см.
Теперь мы можем найти площадь треугольника по той же формуле, что и в первом случае.
Площадь треугольника DEF равна (1/2) * 6 * 5 = 15 кв.см.

4. Прямоугольник CDGI:
Длина прямоугольника CDGI равна 6 см, так как это основание треугольника DEF. Ширина прямоугольника равна высоте треугольника CGH. Мы уже нашли высоту в предыдущем расчете, это 5 см.
Площадь прямоугольника CDGI равна 6 * 5 = 30 кв.см.

Теперь мы можем найти площадь всего палеограма, просто сложив площади каждой фигуры:
Площадь палеограма = площадь треугольника ABC + площадь треугольника DEF + площадь прямоугольника BDEH + площадь прямоугольника CDGI
Площадь палеограма = 24 кв.см + 15 кв.см + 48 кв.см + 30 кв.см
Площадь палеограма = 117 кв.см.

Итак, площадь палеограма, изображенного на рисунке, равна 117 квадратных сантиметров.