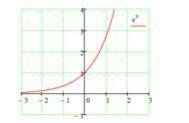
Найдите площадь фигуры ограниченной линиями y=e^x, x=0, x=1, y=0

alexboyko95 1 04.07.2020 12:17 0

Question

Математика: Найдите площадь фигуры ограниченной линиями y=e^x, x=0, x=1, y=0

alexboyko95 · Answer

Площадь криволинейной трапеции равна определённому интегралу.

$S= \int\limits^1_0 {e^{x} } \, dx$

Для вычисления находим первообразную. Первообразной e^x является e^x

Далее вычисляем значение интеграла. Для этого подставляем значение верхнего предела в e^x и вычитаем e^x с подставленным нижним пределом.

$e^{1} - e^{0} = e - 1 = 2,7 -1 = 1,7$

Найдите площадь фигуры ограниченной линиями y=e^x, x=0, x=1, y=0