Найдите площадь фигуры, ограниченной линиями y=e^x-e^-x, x=ln 2, x=ln 3,y=0
Другие вопросы по теме Математика
Популярные вопросы
- оцiнiть периметр Р рiвностороннього трикутника зi стороною а см, якщо...
1 - 1.У чому полягає особливості демократизації в Україні? 2.Децентралізація...
3 - В ряд выписана сумма 105 единиц: 1 + 1 + ... + 1 + 1. Сначала меняют...
2 - 10. Выбери все слова с ударным звуком [а] А) яблоня, поплавать, виноградБ)...
2 - Упр 507 507. Выборочное списывание. Выпишите словосочетания с именами...
3 - МАТЕМАТИКА хэлп на фотке18 ; 20...
1 - Який заряд рухається по провіднику на протязі 5 хв якщо сила струму...
1 - 1.Себеп-салдар салалас сөйлемдер және олардың байланысу жолдары Себеп-салдар...
3 - (13/27+2/9) -(11/21+1/7) как решить...
1 - Длина гардины 1м20см. На каком расстоянии нужно развести 9 колец,...
2
ответ: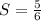 .
.
Пошаговое объяснение:
ответ: во вложении Пошаговое объяснение: