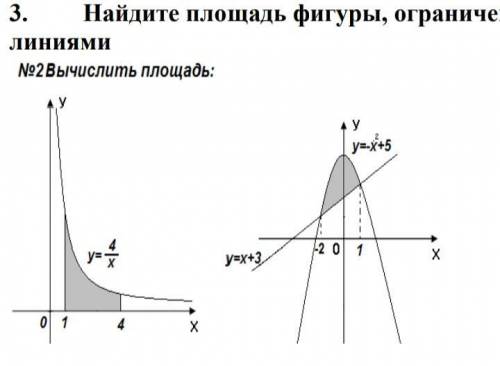
Найдите площадь фигуры, ограниченной линиями )

Добрый день! Конечно, я могу помочь вам найти площадь этой фигуры.

Для начала посмотрим, какие линии ограничивают эту фигуру. Мы видим, что фигуры ограничивают две прямые линии справа и слева, а также дуга, которая соединяет эти две линии.

Для того чтобы найти площадь этой фигуры, мы можем разделить ее на несколько более простых фигур и найти их площади по отдельности. Давайте попробуем.

Для начала давайте посмотрим на большую прямоугольную фигуру, которую можно разделить на две части - верхнюю и нижнюю. Чтобы найти площадь верхней части, нужно найти площадь всей прямоугольной фигуры и вычесть площадь нижней части.

Чтобы найти площадь прямоугольника, нужно умножить его длину на ширину. Давайте измерим длину большой прямоугольной фигуры. Здесь длина прямоугольника равна 10 см. Теперь оценим ширину. Чтобы это сделать, рассмотрим линию слева и линию справа. Каждая из них равна 5 см, поэтому суммарная ширина прямоугольника равна 5+5=10 см.

Теперь, чтобы найти площадь всей прямоугольной фигуры, умножим длину на ширину: 10 см * 10 см = 100 см².

Теперь давайте рассмотрим нижнюю часть фигуры. Она представляет собой сегмент (часть) круга. Для того чтобы найти площадь сегмента, мы можем найти площадь всего круга и вычесть площадь треугольника внутри сегмента.

Чтобы найти площадь круга, нам нужно воспользоваться формулой: S = π * r², где "S" - площадь, "π" - число пи (примерно равно 3.14), "r" - радиус круга. В данном случае радиус круга равен половине длины большой прямоугольной фигуры, то есть 10 см / 2 = 5 см.

Таким образом, площадь всего круга составит S = 3.14 * 5² = 3.14 * 25 = 78.5 см².

Теперь нужно найти площадь треугольника внутри сегмента. Простая формула для нахождения площади треугольника - это площадь равна половине произведения длины основания треугольника на его высоту. Для этого нам нужно найти длину основания треугольника. Основание треугольника представляет собой отрезок между концами линии справа и линии слева. Согласно изображению, это 4 см.

Теперь необходимо найти высоту треугольника. Высота треугольника - это расстояние от середины основания до верхней точки сегмента круга. Это расстояние составляет радиус круга минус расстояние от середины основания до конца линии справа, или (5 см - 1 см) = 4 см.

Теперь, используя формулу для площади треугольника, найдем его площадь: S = 1/2 * b * h = 1/2 * 4 см * 4 см = 8 см².

Теперь у нас есть площадь всего круга (78.5 см²) и площадь треугольника внутри сегмента (8 см²). Чтобы найти площадь нижней части фигуры, нужно вычесть площадь треугольника из площади всего круга: 78.5 см² - 8 см² = 70.5 см².

Теперь, чтобы найти площадь этой фигуры в целом, нужно вычесть площадь нижней части из площади всей прямоугольной фигуры: 100 см² - 70.5 см² = 29.5 см².

Итак, площадь фигуры, ограниченной линиями на данном изображении, равна 29.5 квадратных сантиметров.

Я надеюсь, что объяснение было понятным и полезным для вас. Если у вас возникнут еще вопросы, не стесняйтесь задавать их!