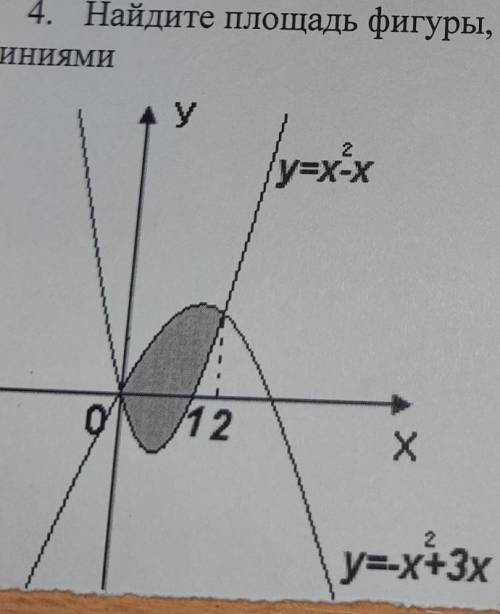
Найдите площадь фигуры ограниченной линиями​

ответ:      S = 1 5/6 кв.од.

Пошаговое объяснение:

f₁(x) = x²- x  ;   f₂(x) = - x² + 3x . Площу фігури можна обчислити так :

S = ∫₀²[ f₂(x) - f₁(x) ]dx - ∫₁²f₁(x)dx ;   маємо :

S = ∫₀²(- x² + 3x - x² + x )dx -  ∫₁²( x² - x )dx = ∫₀²(- 2x² + 4x )dx -  ∫₁²( x² - x )dx =

= ( - 2*x³/3 + 4*x²/2 )│ ₀² - ( x³/3 - x²/2 )│₁² = ( - 2/3 *2³ + 2*2² ) - ( - 2/3*0³ +

+ 2*0² ) - [ ( 2³/3 - 2²/2 ) - ( 1³ /3 - 1² /2 ) ] = - 16/3 + 8 - ( 8/3 - 2 - 1/3 + 1/2 ) =

= - 16/3 + 8 - 8/3 + 2 + 1/3 - 1/2 = - 23/3 + 9 1/2 = -7 2/3 + 9 1/2 = 1 5/6 (кв.од. )