Найдите площадь боковой поверхности правильной четырехугольной усечённой пирамиды стороны оснований которой равны 6 и 22 см, а боковое ребро 4 корень из 5 см.
Другие вопросы по теме Математика
Популярные вопросы
- Сила тока в электрической печи для плавки металла равна 850а при...
1 - Наконец монументальное полотно завершено , плод двадцатилетнего...
3 - Распредели слова по столбикам а : матириал из которово сделан...
3 - Найдите значение выражения: (3-95/21): 16/21...
2 - Боковые ребра попвильной треугольной пирамиды равны 2,5 а апофема...
1 - Известно,что любой организмв своем индивидуальном развитии повторяет...
3 - Бассейн, имеющий форму прямоугольника параллелепипеда, вмещает...
2 - Перевести на казахский о том, как мы отдыхаем. по вечерам папа...
3 - Диаграмма данные на которой изображаются в виде секторов круга...
1 - Подготовьте сообщение о героях рассказа возвращение...
1
Пусть дана правильная четырехугольная усеченная пирамида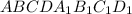 , где
, где 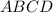 и
и 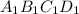 — квадраты со сторонами соответственно 22 см и 6 см. Боковое ребро пирамиды
— квадраты со сторонами соответственно 22 см и 6 см. Боковое ребро пирамиды 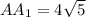 см.
см.
Найдем площадь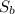 боковой поверхности заданной пирамиды.
боковой поверхности заданной пирамиды.
Для того чтобы ее найти, следует найти площадь одной боковой грани (равнобедренной трапеции) и ее умножить на 4.
Рассмотрим равнобедренную трапецию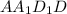
Проведем в трапеции высоту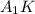
Найдем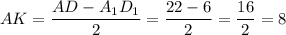 см
см
Рассмотрим прямоугольный треугольник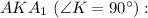
По теореме Пифагора: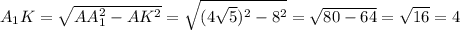 см.
см.
Следовательно, площадь трапеции равна
Таким образом,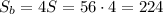 см².
см².
ответ: 224 см².