Найдите периметр прямоугольника, если сумма трех его сторон равна 2k, а площадь наибольшая

3k

Пошаговое объяснение:

Пусть периметр нашего прямоугольника равен Р. Тогда одна из сторон - Р-2k, так как 2k - сумма трех из четырех сторон прямоугольника.

А сумма двух не противоположных сторон равна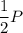   только потому, что Р = а + b + a + b = 2(a + b)

Но так как мы уже знаем одну сторону, мы можем найти и вторую

Площадь прямоугольника - произведение его сторон.

Тогда составим функцию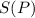 которая будет выражать площадь.

Максимум этой функции - такая точка Р, где площадь наибольшая.

Так как относительно Р данная функция является квадратичной, то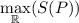 находится легко. Так как у графика данной функции (параболы) ветви опущены вниз (из-за отрицательности коэффициента перед 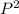-  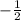), то максимум данной функции находится в вершине, абсцисса (нужное значение Р) которой вычисляется по формуле 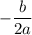( если надо вывести, напишите)

Для нашей функции -

(коэффициенты перед Р и Р² соответственно)

Тогда находим нужное нам значение периметра!

Р.S. Задающий, это просто гениальный (естественно в хорошем смысле) поступок! Не писать варианты ответов! МОЛОДЕЦ!