Найдите периметр прямоугольника, если его диагональ равна 13, а его площадь 60 см в квадрате - на систему уравнения
Другие вопросы по теме Математика
Популярные вопросы
- 1) В треугольниках ABC и DEF сторона AB равна DE, углы A и B равны соответственно...
2 - Кто хорошо знает химию. Решите это уравнение, я в ней полный 0....
1 - Який з уривків є періодом, обгрунтуйте свою думку...
1 - написать сравнительную характеристику Шерлока Холмса і доктора Ватсона...
1 - До ть будь ласка!! У 200г води при температурі 80 С розчиняли 161,6 г натрій...
3 - Отмена крепостного права в прибалтике, эстляндии, Курляндии и лифляндии...
2 - Кальций и Селен 1.Название элемента 2.Химический знак, относительная атомная...
1 - А1. Найдите угловой коэффициент касательной, проведенной к графику функции...
2 - 3,68:9,2=?0,0162:0,3=?10,2*1,2=?Столбиком...
2 - Теория вероятностей. На п яти однакових кульках написані числа 1, 2, 3,...
3
Пусть одна сторона прямоугольника, а также прямоугольного треугольника - х, а другая сторона прямоугольника, а также прямоугольного треугольника - у.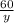
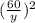 + у² = 169
+ у² = 169
Составим и решим систему уравнений:
х * у = 60 (формула нахождения площади прямоугольника)
х² + у² = 13² (теорема Пифагора)
Выразим из первого уравнения х и подставим во второе:
х =
х =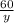
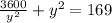
Решаем второе уравнение:
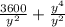
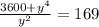
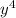 = 169y²
= 169y²
3600 +
y⁴ - 169y² + 3600 = 0
По теореме Виетта:
у₁² = 25
у₁ = 5;
у₂² = 144
у₂ = 12;
Находим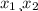 путем подстановки у в первое уравнение:
путем подстановки у в первое уравнение: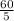
х₁ =
х₁ = 12;
х₂ =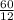
х₂ = 5.
Следовательно, стороны прямоугольника равны 5 см и 12 см.
Теперь находим периметр прямоугольника:
P = (5 + 12) * 2 = 34 см.
ответ: Периметр прямоугольника равен 34 см.