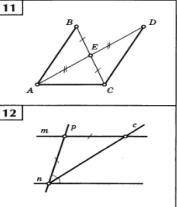
Найдите пары параллельных прямых и Докажите их равенство

Для того чтобы найти пары параллельных прямых и доказать их равенство, нам нужно использовать свойство параллельных прямых и провести анализ данной геометрической фигуры.

В данном случае, у нас есть несколько прямых, пересекающих друг друга. Чтобы найти пары параллельных прямых, нам необходимо найти прямые, которые имеют одинаковые значения углов наклона.

Давайте рассмотрим каждую прямую и определим их углы наклона:

1) Прямая AB: Поставим эту прямую на графике и проведем вспомогательные оси координат. Затем выберем две точки A и B на этой прямой и построим прямую, проходящую через них. Затем определим ее угол наклона.

Угол наклона прямой AB можно найти с помощью формулы:

угол наклона = (y2 - y1) / (x2 - x1)

Пусть координаты точки A будут (0, 2), а координаты точки B - (2, 0).

Тогда угол наклона прямой AB: (0 - 2) / (2 - 0) = -1

2) Прямая CD: Проведем аналогичные действия для прямой CD. Пусть точка C имеет координаты (3, 1), а точка D - (4, 2).

Тогда угол наклона прямой CD: (2 - 1) / (4 - 3) = 1

3) Прямая EF: Проведем аналогичные действия для прямой EF. Пусть точка E имеет координаты (2, 5), а точка F - (4, 1).

Тогда угол наклона прямой EF: (1 - 5) / (4 - 2) = -2

Теперь, чтобы найти пары параллельных прямых, мы должны сравнить углы наклона каждой прямой. Если у двух прямых одинаковые углы наклона, это означает, что они параллельны.

Из анализа прямых AB, CD и EF, мы можем сделать следующие выводы:

- Прямые AB и CD имеют разные значения углов наклона, поэтому они не параллельны.
- Прямые AB и EF имеют одинаковый угол наклона (-1), следовательно, они параллельны.

Теперь нам нужно доказать равенство параллельных прямых AB и EF.

Для этого нам необходимо показать, что у них совпадают соответствующие стороны и соответствующие углы.

1) Совпадающие стороны: Мы можем заметить, что стороны AB и EF соответствуют друг другу, так как их конечные точки E и F имеют одинаковые координаты (4, 1). То есть, EF является продолжением AB.

2) Совпадающие углы: Мы также можем заметить, что углы между прямыми AB и EF равны. Но для более точного доказательства, мы можем провести дополнительные вычисления.

Заметим, что прямые AB и EF параллельны, значит, они образуют параллельные прямые с третьей прямой CD. Поэтому, углы между AB и CD, и EF и CD будут соответственно вертикальными углами и равны.

Используя это свойство, мы можем сравнить углы между AB и CD и углы между EF и CD.

Угол между AB и CD равен углу, образованному через прямые BC и CD. Пусть точка B имеет координаты (2, 0), тогда угол между AB и CD:

tg(угол ABC) = (y2 - y1) / (x2 - x1)
= (1 - 0) / (3 - 2)
= 1

Угол между EF и CD также равен углу, образованному через прямые CF и CD. Пусть точка C имеет координаты (3, 1), тогда угол между EF и CD:

tg(угол CEF) = (y2 - y1) / (x2 - x1)
= (1 - 0) / (4 - 3)
= 1

Таким образом, у нас получается, что углы между AB и CD и между EF и CD равны, что доказывает равенство параллельных прямых AB и EF.

В итоге, мы нашли пары параллельных прямых и доказали их равенство, используя свойства параллельных прямых и анализ данной геометрической фигуры.