Найдите общее и частное решение дифференциального уравнения: xy'+y=x^2,если y=2,при x=1 можно по-подробней,? заранее .
Ответы
ЛНДУ 1-го порядка:
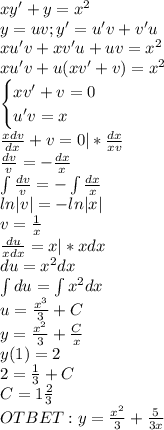
ПОКАЗАТЬ ОТВЕТЫ
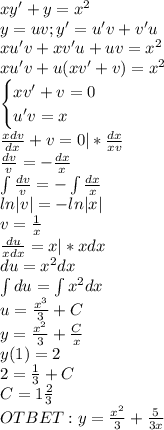
Другие вопросы по теме Математика
Популярные вопросы
- Решите уравнение : 25/2: 5/2=50/3: y...
1 - Подчеркните буквы которые обозначают мягкие согласные.лиса роет нору...
2 - Как составить звуковую схему ! лимон и рулон...
2 - Найдите значение выражения 11/4+6/5...
1 - Составь и запиши словосочетания из данных слов. запиши в скобках вопрос...
3 - Вычислите количество теплоты,необходимое для плавления 1 кг льда,взятого...
2 - Запаліть свічку що ви гаєте плавлення парафіну свічки ці фізичні чи хімічні...
1 - Почему слово знает пишется с буквой е слово дышится с буквой и слово...
2 - Что укрошало дом извесного композитора эдварда грига...
3 - Какие образования слов вы знаете кроме как приставочный , суффиксальный...
2