Найдите область значений функции f(x)=3cosx-4sinx+3

f(x)=3cosx-4sinx+3

Выражение 3cosx-4sinx преобразуем при тождества asinx - bcosx = √(a² + b²)sin(x-arcsin(b/√(a² + b²))), где √(a² + b²) = √(4² + 3²) = √25 = 5; arcsin(b/√(a² + b²)) = arcsin(4/5). Имеем:

f(x)=3cosx-4sinx+3 = -4sinx + 3cosx +3 = 5·sin(x-arcsin(4/5)) + 3.

Значение этого выражения зависит только от первого слагаемого.

-1 ≤ sin(x-arcsin(4/5)) ≤ 1|·5; -5 ≤ 5sin(x-arcsin(4/5)) ≤ 5|+3;

-2 ≤ 5sin(x-arcsin(4/5)) + 3 ≤ 8. Т.е. -2 ≤ f(x) ≤ 8.

ответ: Е(f) = [-2; 8].

f(x)=3cosx-4sinx+3 =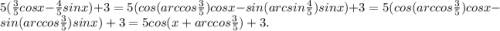

-1 ≤ cos(x + arccos0,6) ≤ 1|·5; -5 ≤ 5cos(x + arccos0,6) ≤ 5| +3;

-2 ≤ 5cos(x + arccos0,6) + 3 ≤ 8; -2 ≤ f(x) ≤ 8.

ответ: E(f) = [-2; 8].