Найдите область сходимости ряда.
Буду всем сердцем благодарна тому, кто сможет это решить!)

Найдите область сходимости ряда. Буду всем сердцем благодарна тому, кто сможет это решить!)

Ответы

Діанка465 02.05.2021 19:51

Пошаговое объяснение:

это степенной ряд. запишем его в общем виде

$\displaystyle \sum\limits_{n=1}^{\infty}\frac{1}{n^5*7^n} x^n$

областью сходимости степенного ряда является интервал (-R;R), где R - радиус сходимости и равен

$\displaystyle R = \lim_{n \to \infty} \frac{a_n}{a_{n+1}}$

посчитаем этот предел

$\displaystyle \lim_{n \to \infty} \bigg (\frac{7*7^n(n+1)^5}{7^nn^5} \bigg )=7$

таким образом, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-7;7)

теперь посмотрим сходимость ряда на концах этого интервала.

пусть х = -7, тогда мы получим ряд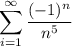 $\displaystyle \sum \limits_{i=1}^{\infty}\frac{(-1)^n}{n^5}$ , это числовой знакочередующийся ряд

надо исследовать его на сходимость. исследуем по признаку Лейбница

а) по первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего

$\displaystyle 1\frac{1}{32} \frac{1}{243}$ - выполняется

б) по второму признаку Лейбница предел ряда по модулю должен стремится к 0

$\displaystyle \lim_{n \to \infty} \frac{1}{n^5} =0$ выполняется

т.е. ряд сходится x = -7 - точка сходимости

теперь пусть х = 7

тогда всё просто, как в первом случае, только ряд не знакочередующийся. он сходится x = 7 - точка сходимости

и вот получаем,

данный степенной ряд является сходящимся на интервале [-7;7]

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

Shnella 01.06.2019 15:00

kykapeka227 01.06.2019 15:00

Vesthumer 01.06.2019 15:10

Катя46811909 01.06.2019 15:10

milanaberezova 01.06.2019 15:10

putnikputen 01.06.2019 15:10

Nikita20330 01.06.2019 15:10

Pomogatorr 01.06.2019 15:10

mr20171 01.06.2019 15:10

Решите уравнение: х +6/35 = 12/15х +...

АндрейПермь123 01.06.2019 15:10

6/7 : 3 сколько будет можно с решением...