Найдите, область определения функции (на картинке) : 3
+ и

1)

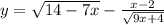
Область определения этой функции должна удовлетворять двум условиям:

1) подкоренное выражение неотрицательно (т.е. 14 - 7х ≥ 0 и 9х + 4 ≥ 0)

2) знаменатель дроби отличен от нуля (т.е. )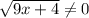

Поэтому эти условия удобно записать в виде системы:

Решением системы неравенств будет множество, которое и есть область определения функции.

ответ:

2) Рисунок к задаче - во вложении.

Проведем отрезки BD и AC.

Получим, что ΔABD=ΔCDB по трем сторонам (BD-общая, CB=AD, CD=AB) и ΔCDA=ΔABC по трем сторонам (AC-общая, CB=AD, CD=AB).

Из равенства ΔABD и ΔCDB следует, что соответственно равны ∠A и ∠C.

А из равенства ΔCDA и ΔABC следует, что соответственно равны ∠D и ∠B.

Наконец, рассмотрим ΔCOB и ΔAOD. У них CB=AD, ∠A=∠C, ∠В=∠D. Значит, ΔCOB = ΔAOD по стороне и прилежащим к ней углам.

Из равенства ΔCOB и ΔAOD следует равенство соответственных сторон СО и AO.

Доказано.