Найдите объем тела, ограниченного поверхностями, заданными уравнениями
Другие вопросы по теме Математика
Популярные вопросы
- How we will celebrate friendship day...
2 - Оксиды 1.оксиды состоят из кислорода и: а) одного элемента б) двух элементов...
1 - Объясните значение слов : мольба. хватит киснуть. нелепый. доходяга....
3 - Объясните, что такое честолюбие и самолюбие. в чем разница между этими...
3 - Разбор предложения светлеет воздух,яснеет небо,белеют тучки,зеленеют...
1 - H3aso4,h3po3,h3po4,hno3 какая из этих кислот самая сильная...
3 - Алиса, шляпник и кролик сели пить чай. чеширский кот пить чай чеширский...
1 - Вырази: 3 м в квадрате= в квадрате 900 см в квадрате= в квадрате 80...
1 - Сөзге морфологиялық талдау жаса. қша...
3 - Составьте квадратное уравнение ,корни которого равны 3-корень из 2 и...
2
Найдем кривые пересечения плоскостей: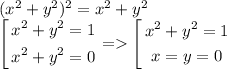
Вычисление интеграла в приложении.