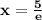Найдите наименьшее значение функции y= xlnx - xln5 на отрезке [1; 5]
Другие вопросы по теме Математика
Популярные вопросы
- Напишите письмо другу,и поделитесь впечатлениями о книге :who the book...
1 - Краткое содержание о книге трудно быть другом ( Виктор Штанько)...
2 - Визначте дослідника маршрути мандрівок якого наведені на фрагменті...
1 - У трикутника дві сторони дорівнюють 6см і 12см а кут між ними 120 Знайти...
1 - До ть потрібно розкласти на множники...
2 - . Під час зважування металевої кулі на нерівноплечих важільних терезах...
1 - 7КЛАС. У зрівноваженій системі (блок, мотузки і пружина невагомі) визначте...
1 - Масса слонихи со слоненком 7 Т 200 кг Какова масса слонёнка если он...
1 - 1. Укажите верное утверждение. а. Через любые три точки можно провести...
3 - Нужно ОЧЕНЬ краткое содержание пьесы Бесприданница ...
1
Находим производную Y`=x*1/x-x*1/5=0
1-x/5=0 x=5, когда на оси находим знаки производной получается с плюса на минус ,поэтому эта точка и является точкой минимума, х=5
наименьшее значение функции достигается при