Найдите наименьшее значение функции y=7x-ln(x+4)^7 на отрезке (-3,5; 0)
Другие вопросы по теме Математика
Популярные вопросы
- Решить ! за контрольную работу 6 человек получили отметку 5 , 10 человек -- 4 ,...
1 - Фонетический разбор слова солнце и ярко....
2 - Для определения зависимости рек от климата проведите исследование по картам. для...
1 - Текст қазақ тілі сабағында минимум...
2 - 1)4cosx = sin2x 2)найдите tga, если cosa=1/(sqrt10) и a принадлежит промежутку...
1 - Главные части термометра - стеклянная трубка, наполненная жидкостью, и шкала (пластинка...
2 - )осуществите превращения: al - na[al(oh)4] - al(oh)3 - na[al(oh)4] - al2(so4)3...
1 - 16x- x в кубе нужно разложить на множители...
3 - Десять любых слов разбор по составу !...
1 - Перевести на ., сделать отрицание, 5 типов вопросов (общий, выбор - or, специальный,...
1
y’=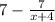
Найдем точки экстремум:
ОДЗ:
x≠-4
Подставим значения краев данных отрезков и точку экстремум:
______
______
Соответственно наименьшее значение данная функция на заданном отрезке принимает в точке (-3) и оно равняется -21.
ответ: -21
-21
Пошаговое объяснение:
Найдите наименьшее значение функции y=7·x-ln(x+4)⁷ на отрезке [-3,5;0].
1) ОДЗ: x+4>0 ⇔ x>-4 ⇔ x∈(-4; +∞). Отрезок [-3,5;0] является подмножеством (-4; +∞).
2) Находим производную от функции y=7·x-ln(x+4)⁷ = 7·x-7·ln(x+4):
3) Находим критические точки из отрезка [-3,5;0] . Для этого находим нули производной:
4) Вычислим значения функции при x= -3,5, x= -3, x= 0:
y(-3,5)=7·(-3,5)-7·ln(-3,5+4)= -24,5-7·ln0,5
y(-3)=7·(-3)-7·ln(-3+4)= -21-7·ln1= -21
y(0)=7·0-7·ln(0+4)= -7·ln4
5) Сравним значения функции при x= -3,5, x= -3, x= 0 и определим наименьшее:
y(0)-y(-3,5) = -7·ln4-(-24,5-7·ln0,5) = -7·ln4+24,5+7·ln0,5 = -7·ln4+24,5-7·ln2 =
= 24,5-7·(ln4+ln2) = 24,5-7·ln8 = 24,5-7·ln8 > 24,5-7·lne³ = 24,5-7·3=3,5>0,
то есть y(0) > y(-3,5);
y(0)-y(-3) = -7·ln4-(-21) = 21-7·ln4 = 21-7·lne² = 21-7·2=7>0,
то есть y(0) > y(-3);
y(-3)-y(-3,5) = -21-(-24,5-7·ln0,5) = -21+24,5+7·ln0,5=3,5-7·ln2=3,5·lne-7·ln2=
= 3,5·(lne-ln2²) = 3,5·(lne-ln4) = 3,5·ln(e/4) = -3,5·ln(4/e) <0,
то есть y(-3) < y(-3,5).
Отсюда:
y(-3) < y(-3,5) < y(0)
и наименьшее значение функции равен -21.